Опубликовано Автор: alexxlab Категории: Разное

Содержание

Математики совершили новое открытие, связанное с додекаэдром / Хабр

Трое математиков получили ответ на фундаментальный вопрос о прямых путях на 12-гранном платоновом теле


Несмотря на то, что математики уже более 2000 лет [а, возможно, и ещё больше / прим. перев.] разбирают структуру пяти правильных многогранников (платоновых тел) – тетраэдра, гексаэдра (куба), октаэдра, додекаэдра и икосаэдра – мы ещё очень многого о них не знаем.

И вот трое математиков ответили на один из самых базовых вопросов, касающихся додекаэдра.

Допустим, вы стоите на одной из вершин правильного многогранника. Существует ли прямой путь, по которому можно вернуться в точку старта, не проходя ни через одну из остальных вершин? Для четырёх других правильных многогранников, составленных из квадратов или равносторонних треугольников — тетраэдра, куба, октаэдра и икосаэдра – математики недавно дали отрицательный ответ на этот вопрос. Любой прямой путь, начинающийся с одной из вершин, либо наткнётся на другую вершину, либо будет вечно виться по поверхности фигуры, так и не вернувшись в исходную точку.

Однако математики не знали, чего можно ожидать от додекаэдра, состоящего из 12 пятиугольников.

Теперь Джейдев Атрейа, Дэвид Оличино и Патрик Хупер показали, что на додекаэдре действительно существует бесконечное множество подобных путей. В их работе, опубликованной в мае в журнале Experimental Mathematics, показано, что эти пути можно естественным способом разделить на 31 семейство.

Поиск решения потребовал использования современных технологий и составления компьютерных алгоритмов. «Лет двадцать назад этот вопрос был вне досягаемости; лет 10 назад он потребовал бы невероятных усилий по написанию всех необходимых программ; и только сегодня все факторы сошлись», — написал в емейле Антон Зорич из Математического института Жасси в Париже.

Этот проект стартовал в 2016 году, когда Атрейа из Вашингтонского университета и Оличино из Бруклинского колледжа начали играться с набором плоских фигур, складывавшихся в правильный многогранник. Во время сборки многогранника Оличино понял, что накопленный за последнее время материал по плоской геометрии может оказаться кстати для понимания прямых путей на додекаэдре.

«Мы буквально собирали эти штуки из разрозненных кусочков, — сказал Атрейа. – Простое любопытство исследователей совпало с новой возможностью».

Вместе с Хупером из Сити-колледжа в Нью-Йорке исследователи придумали, как классифицировать все прямые пути, выходящие из одного из углов и приходящие в него же, минуя остальные углы.

Их анализ является «элегантным решением», как выразился Говард Мазур из Чикагского университета. «Это один из тех случаев, когда я без колебаний могу заявить: Вот это да, почему же я этого не сделал!»

Скрытые симметрии

Хотя математики уже более ста лет рассуждают о прямых путях на додекаэдре, в последние годы интерес к этой теме возродился благодаря полученным недавно новым знаниям в области «поверхностей переноса». Такие поверхности формируются при помощи склейки параллельных сторон многогранника. Они оказались очень полезными для изучения широкого спектра тем, связанных с прямыми путями, идущими по фигурам с углами – от

траекторий биллиардных шаров

до вопросов о том, может ли один луч света

осветить всю комнату

с зеркальными стенками.

Базовая идея во всех этих задачах – так развернуть фигуру, чтобы идущие по ней пути стало проще изучать. Чтобы разобраться в прямых путях, идущим по правильному многограннику, можно начать с разрезания достаточного количества рёбер для того, чтобы их можно было развернуть на плоскости, сформировав, как говорят математики, сеть. Одна из сетей для куба, к примеру – фигура в виде буквы «Т», состоящая из шести квадратов.


Додекаэдр из бумаги, сделанный в 2018 году Дэвидом Оличиной и Джейдевом Атрейей для демонстрации возможности провести путь из одной вершины обратно в неё же без пересечения других.

Представьте, что мы сделали развёртку додекаэдра, и теперь идём по ней в некоем выбранном направлении. Рано или поздно мы наткнёмся на ребро сети, после чего наш путь перепрыгнет на соседний пятиугольник (тот, что был приклеен к текущему до того, как мы разрезали наш додекаэдр). При прыжке путь одновременно поворачивается на некий угол, величина которого в градусах делится на 36.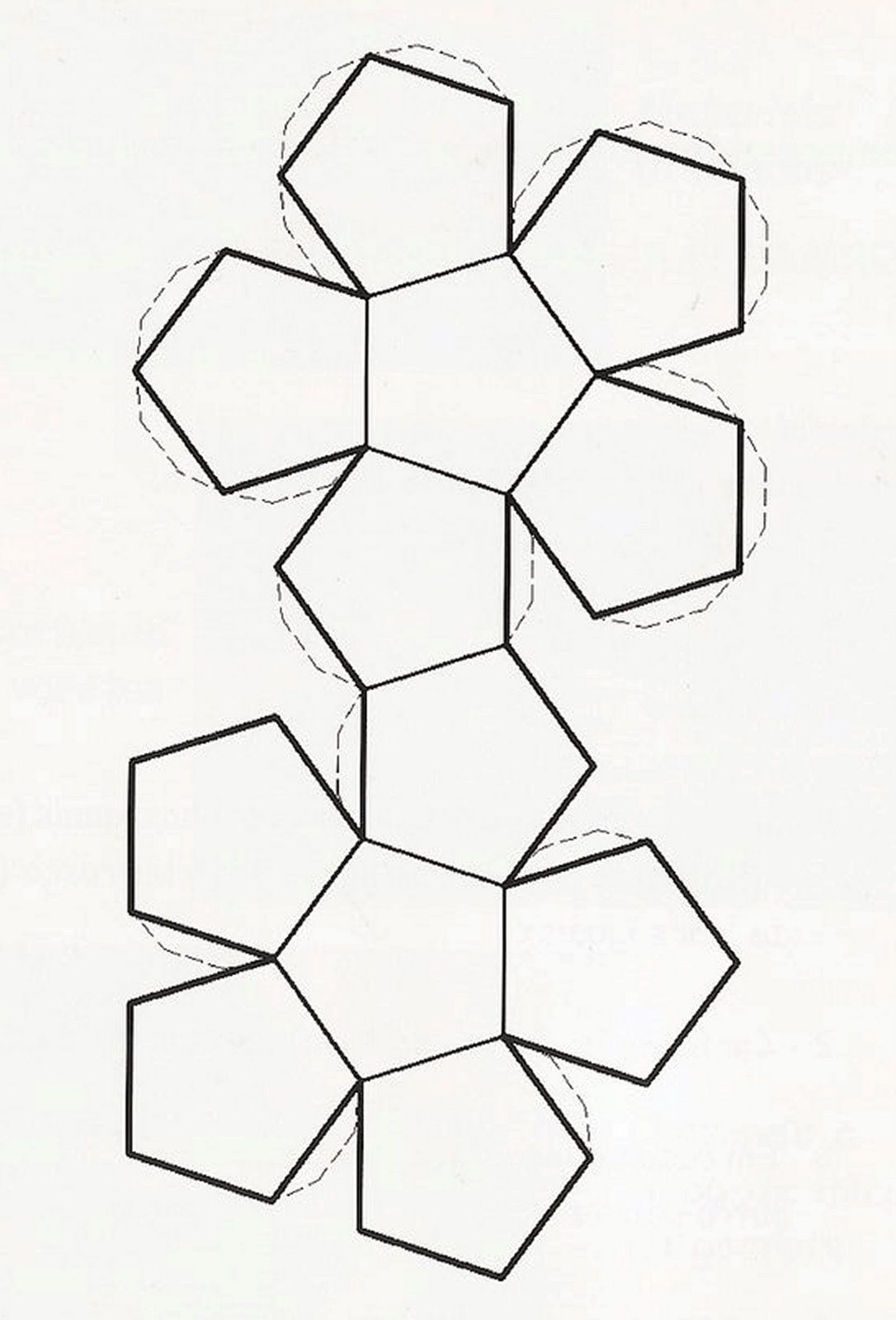

Чтобы избежать всех этих прыжков и поворотов, при встрече с ребром мы могли бы приклеить на него новую, повёрнутую копию сети, и продолжать идти прямо. Тогда у нас добавится избыточности: у нас будет два разных пятиугольника, обозначающих пятиугольник оригинального додекаэдра. Мы усложнили наш мир, но упростили наш путь. Мы можем продолжать добавлять новую сеть каждый раз, когда нам необходимо выйти за границы нашего мира.

К тому времени, как наш путь пройдёт через 10 сетей, мы повернём нашу оригинальную сеть на все возможные варианты углов, делящиеся на 36, и ориентация следующей добавленной нами сети совпадёт с той, с которой мы начинали. Получается, что 11-я сеть получается из оригинальной простым сдвигом – как говорят математики, переносом. Вместо того, чтобы приклеивать 11-ю сеть, мы можем просто приклеить ребро 10-й сети к соответствующему параллельному ребру оригинальной сети. Наша фигура уже не будет плоской, но математики считают, что она «помнит» плоскую геометрию своего предыдущего воплощения – так что, к примеру, пути считаются прямыми, если они были прямыми на ещё не склеенной фигура. После того, как мы сделаем все возможные склейки соответствующих параллельных рёбер, мы получим т.н. поверхность переноса.


Атрейа на правой руке сделал себе татуировку своей любимой поверхности переноса – двойного пятиугольника

Полученная поверхность — это представление додекаэдра, сделанное с большой избыточностью, в котором участвует 10 копий каждого пятиугольника. И оно гораздо получилось более сложным – оно склеено в виде пончика с 81 отверстиями. Тем не менее, эта сложная форма позволила троим исследователям разобраться в богатой теории поверхностей переноса.

Столкнувшись с такой гигантской поверхностью, математики закатали рукава – как фигурально, так и буквально. Поработав с ней несколько месяцев, они поняли, что поверхность пончика с 81 отверстием формирует избыточную презентацию не только додекаэдра, но и одной из самых часто изучаемых поверхностей переноса. Это двойной пятиугольник, который получается, если склеить два пятиугольника по одному из рёбер, а затем склеить все идущие параллельно стороны, чтобы получился пончик с двумя отверстиями и большим набором симметрий.

Также эта фигура вытатуирована на руке Атрейи. «Я уже знал и любил этот двойной пятиугольник», — сказал Атрейа, сделавший эту татуировку за год до того, как они с Оличино начали размышлять о додекаэдре.

Поскольку двойной пятиугольник и додекаэдр – геометрические родственники, высокая степень симметричности первого может помочь разобраться в структуре второго. «Это потрясающая скрытая симметрия», — сказал Алекс Эскин из Чикагского университета (консультировавший Атрейю по докторской диссертации 15 лет назад). «То, что у додекаэдра есть такая скрытая группа симметрии, является весьма примечательным фактом».


Джейдев Атрейа рассказывает, как они с коллегами решили давнюю задачу поиска прямых путей на додекаэдре

Взаимосвязь между этими поверхностями позволила исследователям воспользоваться алгоритмом анализа поверхностей переноса с высокой симметричностью, который разработала Мириам Финстер из Технологического института Карлсруэ. Адаптировав её алгоритм, исследователи смогли найти все прямые пути на додекаэдре, выходящие из одной вершины и возвращающиеся в неё, и классифицировать их на основе скрытых симметрий додекаэдра.

Этот анализ Атрейа характеризует как «один из самых интересных проектов за всю мою карьеру». Джейдев говорит, что очень важно постоянно играться с разными вещами.

Новый результат говорит о том, что даже в тех объектах, которые люди изучают уже тысячи лет, могут скрываться секреты, сказал Эскин. «Думаю, что даже для этих троих математиков было неожиданностью то, что они смогли сказать что-то новое по поводу додекаэдра».

Додекаэдр

Додекаэдр

Высшее назначение математики- находить порядок в хаосе, который нас окружает
Норберт Винер

Правильные многогранники привлекают совершенством своих форм, полной симметричностью. Кристалл пирита (сернистый колчедан FeS) — природная модель додекаэдра.

Вирус полиомиелита имеет форму додекаэдра. Он может жить и размножаться только в клетках человека и приматов. Это, в частности, означает, что заразиться полиомиелитом можно только от людей. Кроме того, многие вирусы передаются через переносчиков, роль которых нередко выполняют членистоногие (например, клещи). Такие вирусы могут иметь широкий спектр хозяев, включающий как позвоночных, так и беспозвоночных животных. Аденовирусы (от греческого aden — железо и вирусы), семейство ДНК-содержащих вирусов, вызывающих у человека и животных аденовирусные болезни.

Водоросль вольвокс — один из простейших многоклеточных организмов — представляет собой сферическую оболочку, сложенную в основном семиугольными, шестиугольными и пятиугольными клетками (то есть клетками, имеющими семь, шесть или пять соседних; в каждой «вершине» сходятся три клетки). Бывают экземпляры, у которых есть и четырехугольные, и восьмиугольные клетки, но биологи заметили, что если таких «нестандартных» клеток (менее, чем с пятью и более, чем с семью) сторонами нет, то пятиугольных клеток всегда ровно на двенадцать больше, чем семиугольных (всего клеток может быть несколько сотен и даже тысяч).

Это утверждение следует из известной формулы Эйлера.

Фуллерены – одна из форм углерода. Они были открыты при попытке моделировать процессы, происходящие в космосе. Позже ученым в земных лабораториях удалось синтезировать и исследовать многочисленные производные этих шарообразных молекул. Возникла химия фуллеренов. Некоторые соединения включения в кристаллическую решетку фуллерена С60 оказались «горячими сверхпроводниками» с критической температурой до 117 К. Ведутся попытки создать на основе фуллеренов материалы для зарождающейся молекулярной электроники. Все это интересно и важно. Но фуллерены, как выяснилось, есть и в земных породах.

Методами вычислительного моделирования показана возможность связывания фуллеренов с РНК и двойными спиралями молекулы ДНК. Молекулы ДНК являются одним из центральных компонентов современных технических устройств, используемых для создания биочипов и биосенсоров. Предполагается, что фуллерены смогут существенно модифицировать работу таких устройств.

Сейчас с наличием в шунгитах фуллеренов некоторые энтузиасты связывают целебное действие открытых в 1714 г. марциальных вод, которыми лечился Петр Великий. А последние открытия геохимиков заставляют вернуться к проблеме происхождения фуллеренов. Возможно, что новые химические исследования земных фуллеренов приоткроют другие страницы богатой истории планеты Земля!

В алхимии обычно говорится только об этих элементах: огонь, земля, воздух и вода; редко упоминается эфир ,потому что это настолько священно. В Пифагорейской школе, стоило бы вам только лишь упомянуть за стенами школы слово «додекаэдр», как вас убили бы на месте. Настолько священной считалась эта фигура. О ней даже не говорили. Спустя двести лет, при жизни Платона, о ней говорили, но только очень осторожно. Почему? Потому, что додекаэдр расположен у внешнего края вашего энергетического поля и является высшей формой сознания. Когда вы достигаете 55-футового предела своего энергетического поля, то оно будет иметь форму сферы. Но самая близкая к сфере внутренняя фигура – это додекаэдр (в действительности, додекаэдро-икосаэдральная взаимосвязь). Вдобавок к этому, мы живём внутри большого додекаэдра, который содержит в себе вселенную. Когда ваш ум достигает предела пространства космоса – а предел тут есть – то он натыкается на додекаэдр, замкнутый в сфере. Додекаэдр есть завершающая фигура геометрии и она очень важна.

На микроскопическом уровне, додекаэдр и икосаэдр являются относительными параметрами ДНК, по которым построена вся жизнь. Можно увидеть также, что молекула ДНК представляет собой вращающийся куб. При повороте куба последовательно на 72 градуса по определённой модели, получается икосаэдр, который, в свою очередь, составляет пару додекаэдру. Таким образом, двойная нить спирали ДНК построена по принципу двухстороннего соответствия: за икосаэдром следует додекаэдр, затем опять икосаэдр, и так далее. Это вращение через куб создаёт молекулу ДНК.

В основе структуры ДНК лежит священная геометрия, хотя, могут обнаружиться ещё и другие скрытые взаимосвязи. В книге Дана Уинтера «Математика Сердца» (Dan Winter, Heartmath) показано, что молекула ДНК составлена из взаимоотношений двойственности додекаэдров и икосаэдров.

Живые источники математического творчества
неотделимы от интереса познания природы и
задач управления природными явлениями.

Развертка и схема додэкаэдра. Шаблон и развертка из бумаги или картона, как сделать додекаэдр

Дата публикации: .

Развертка и схемы додекаэдра. Как сделать додекаэдр самому?



Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Скачать: «Число 1, цифра 1» (PPTX)

Развивающие и обучающие пособия в интернет-магазине «Интеграл»
Тренажер по Моро М.И.    Тренажер по Петерсон Л.Г.

Из истории додекаэдра

Каждый, кто учился в школе, изучал геометрию, кто-то ее любил, а кто-то не очень, а кому-то только предстоит познакомиться с этой наукой. И, конечно же, всем задавали нарисовать или собрать различные геометрические фигуры, а потом оценивали лучшую работу. Но, к сожалению не все учителя рассказывают о происхождении геометрических фигур, для чего они нужны, какое значение имеют и где применяются. А у фигур очень богатая история, они важны так же, как и любые открытия в нашем мире. А встречаются они повсюду, просто мы не всегда их замечаем. Сегодня мы расскажем вам о додекаэдре.

Слово додекаэдр имеет греческое происхождение и состоит из 2 слов: dodeka (двенадцать) и hedra (грань). Додекаэдр имеет 12 граней, 20 вершин, в каждой из которых сходиться 3 ребра и 30 рёбер. Сумма плоских углов равна 324°. Это двенадцатигранник, который составлен из двенадцати правильных пятиугольников. Додекаэдр правильный многогранник, он имеет три звездчатые формы.

О додекаэдре было известно уже в древние времена. Например, ученикам Пифагорейской школы запрещалось произносить это слово за пределами школы, так как за это они могли лишиться жизни.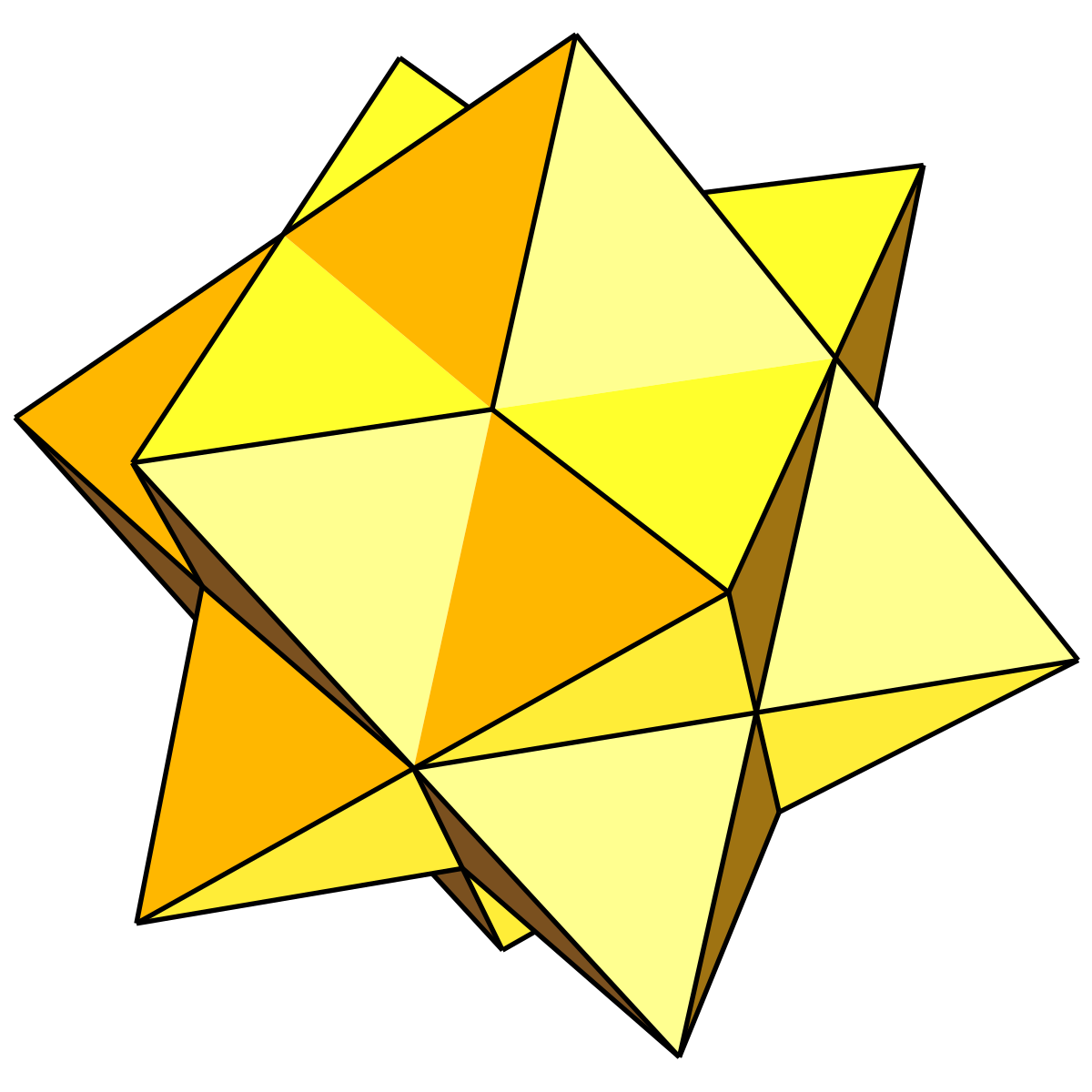 К этой фигуре относились как к святой фигуре, о ней даже боялись что-либо сказать. Лишь спустя двести лет, во времена Платона, об этой фигуре начали очень осторожно говорить. Запрещено было произносить что-то лишнее, тем более оскорбительное или пренебрежительное. Верили в то, что додекаэдр находится в энергетическом поле людей и является высшей формой сознания человека. К тому же считалось, что люди живут внутри огромного додекаэдра, в котором расположена наша вселенная и когда ум человека достигает самого предела пространства Космоса, он натыкается на додекаэдр, замкнутый в сфере.


Додекаэдр в нашей жизни

Где же можно встретить додекаэдр? Подумайте хорошенько! Наверное почти все видели его в качестве генератора случайных чисел, например, по телевизору в игре лото или в настольных ролевых играх. Додекаэдр можно встретить в игре «Пентакор», мир которого представлен в виде этой фигуры. И, конечно же все слышали про Пентагон, это здание Министерства обороны США имеет форму правильного пятиугольника.

В августе 2006 года при нанесении на карты распределения тёмной материи в скоплении галактик, были сделаны выводы, что наша Вселенная выглядит как набор бесконечно повторяющихся додекаэдров.

Правильные многогранники всегда привлекали совершенством своих форм, полной, казалось бы, невозможной симметричностью. Некоторые из таких тел встречаются в природе, например в виде кристаллов, другие — могут быть в виде вирусов или простейших микроорганизмов.

Вирус полиомиелита имеет также форму додекаэдра. Живет, и размножаться только в клетках человека и приматовКристалл пирита (сернистый колчедан) — это природная модель додекаэдра

Собрать эту удивительную фигуру вы можете, используя наши развертки додекаэдра.

Развертка додекаэдра из бумаги или из картона


Схема правильного додекаэдраСхема додекаэдра с формуламиСхема додекаэдра с великими открытиями человечества
JPGJPGJPG
Схема додекаэдра с календарем на 2013 годСхема додекаэдра с героями мультиков
JPGJPG

Многогранная игра, или Как сделать ёжика из додекаэдра

Что вы подумаете, если в глухом лесу увидите на земле квадрат, выложенный из палочек или камней? Вряд ли у вас возникнет мысль, что это сделал какой-нибудь енот или что эта фигура образовалась сама собой. Скорее всего, вы решите, что к созданию квадрата приложил руки человек, ну или заподозрите вмешательство инопланетных существ. В любом случае это непременно должно быть разумное существо. Возможно, разум и вызывает у нас неосознанную симпатию ко всему симметричному. Вот висит на стене картина, вроде бы — какая разница, висит она ровно или один её край чуть выше другого. Но нет, нам это не нравится, и мы обязательно выровняем картину, потому что так красиво, так правильно.

Малый звёздчатый додекаэдр. Фото: Halixi72/Wikimedia Commons/CC-BY-SA-03.

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Принцип построения звёздчатого пятиугольника из правильного пятиугольника.

Малый звёздчатый додекаэдр (вверху), большой додекаэдр (в центре) и большой звёздчатый додекаэдр (внизу).

Головоломка «Звезда Александера». Фото: Hellbus/Wikimedia Commons/CC-BY-SA-3.0.

Единственная форма звёздчатого октаэдра. Фото: Robert Webb’s Stella softwore/Wikimedia Commons/CC-SA-1.0.

Самая первая звёздчатая форма икосаэдра. Фото: Robert Webb/Wikimedia Commons.

Римляне отливали из бронзы додекаэдры. Правда, назначение этих геометрически правильных предметов до сих пор точно не определено. Фото: Lokilech/Wikimedia Commons/CC-BY-SA-3.0.

‹

›

Стремлением к симметричному, ровному особенно сильна геометрия, она изучает, в частности, такие фигуры, как правильные треугольники, правильные многоугольники и правильные многогранники. Ведь куб и вправду смотрится лучше, чем какой-то «неправильный» параллелепипед. А икосаэдр или додекаэдр просто не могут не вызвать тёплых чувств у поклонников стереометрии. О многогранниках, правильных и не очень, мы сегодня и поговорим.

Начнём с «плоского» примера, с правильного многоугольника. Это, как известно, выпуклый многоугольник, у которого равны все стороны и все углы между смежными сторонами. Сколько может быть правильных многоугольников? Да бесконечно много, только по форме они будут всё больше и больше приближаться к окружности. Если вы захотите изобразить правильный тысячеугольник, то просто возьмите в руки циркуль и нарисуйте окружность.

А что будет, если от плоских фигур перейти к объёмным, например попытаться построить разные правильные многогранники?

Тут полёт фантазии придётся ограничить — больше пяти правильных многогранников создать никак не получится. (Кстати, вы можете попробовать самостоятельно доказать столь простую теорему.) Этот факт установили ещё древние греки. Евклид описал все пять правильных многогранников, а Платон использовал их для описания своего представления о строении Вселенной, именно поэтому пятёрку правильных многогранников — тетраэдр, октаэдр, икосаэдр, куб и додекаэдр — называют «платоновы тела». Хотя некоторые из них, к примеру куб, были известны ещё за тысячу лет до древнегреческого мыслителя.

Ну а теперь самое интересное: как превратить додекаэдр в «ёжика»? Сначала нам придётся научиться строить звёздчатые формы многоугольников (рисунок внизу).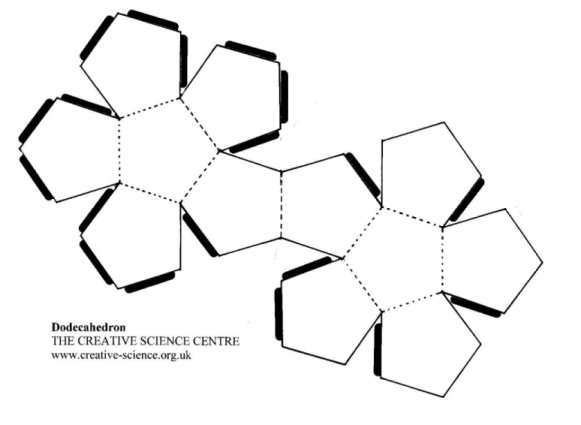 Чтобы получить звёздчатый пятиугольник, нужно продолжить его стороны прямыми линиями до пересечения их друг с другом (новые области окрашены в синий цвет). Соединив между собой вершины звёздчатого пятиугольника, получим правильный пятиугольник (зелёный цвет). Такой процесс можно повторять бесконечное число раз, превращая пятиугольник в звезду и наоборот.

Применим ту же идею, но уже для объёмной фигуры: вместо продолжения линий будем продолжать плоскости граней. Линии пересечения этих плоскостей создадут рёбра нового многогранника. Для построения малого звёздчатого додекаэдра нужно построить правильную пятиугольную пирамиду на каждой грани исходного додекаэдра (рисунок в центре).

Проделав такую процедуру первый раз, мы получим так называемый малый звёздчатый додекаэдр. Его открыл в 1619 году Иоганн Кеплер. Многогранник представляет собой додекаэдр, на гранях которого построены двенадцать пятиугольных пирамид.

Не будем на этом останавливаться и, как в случае с плоским многоугольником, соединим вершины малого звёздчатого додекаэдра. У нас получится большой додекаэдр, честь открытия которого в 1809 году принадлежит Луи Пуансо. Кстати, головоломка, подобная кубику Рубика, — «звезда Александера» выполнена как раз в форме большого додекаэдра.

Продолжив построение подобным образом, получим многогранник с 20 лучами. Эта завершающая звёздчатая форма додекаэдра носит название «большой звёздчатый додекаэдр». Его тоже описал Иоганн Кеплер. Хотя стоит сказать, что подобные фигуры появились ещё до Кеплера, но полное математическое описание дал именно он. Эту фигуру можно назвать многогранным «ёжиком».

У додекаэдра всего три звёздчатые формы: малый звёздчатый додекаэдр, большой додекаэдр и большой звёздчатый додекаэдр. Если соединить вершины большого звёздчатого додекаэдра, то получится тот многогранник, с которого, собственно, и начались наши звёздчатые метаморфорзы, — обычный додекаэдр.

А что с «ёжиками» из других правильных многогранников? Два из нашей «великолепной пятёрки» — тетраэдр и куб — не имеют звёздчатых форм. Как бы вы ни пробовали продолжить грани этих объёмных фигур, ничего не получится. Октаэдру посчастливилось иметь только одну звёздчатую форму — так называемый звёздчатый октаэдр, или Stella octangula — звезда восьмиугольная. Изображение звёздчатого октаэдра, который, по сути, представляет собой два совмещённых тетраэдра, присутствует ещё в работах Леонардо да Винчи, но назвал эту фигуру именно так любитель многогранников Иоганн Кеплер. А вот икосаэдру в плане «звёздности» повезло — у него число звёздчатых форм больше, чем сумма этих форм у всех остальных его правильных многогранных собратьев, — целых 59! Перечислять все мы не будем, ограничимся лишь первой звёздчатой формой.

Красивые звёздчатые многогранники не встречаются в природе, но создать их модели вполне под силу любому школьнику, и бумага здесь — идеальный материал. Разрабатывать развёртку многогранника самому увлекательное, но трудоёмкое занятие, проще воспользоваться специальным конструктором «Волшебные грани». Выбор – 16 интереснейших моделей. Каждый набор содержит комплект деталей из лакированного цветного картона, уже вырезанных и подогнутых. Используя клей и инструкцию, можно создать свою занимательную коллекцию геометрических тел.

Объемный додекаэдр. Геометрические фигуры. Додекаэдр. Как сделать икосаэдр из бумаги: схема

Додекаэдром называется объемная фигура, состоящая из двенадцати пятиугольников. Чтобы получить эту фигуру, необходимо вначале начертить ее развертку на плотной бумаге, а затем собрать ее из этой развертки в пространстве.

Вам понадобится

  • — плотная бумага;
  • — карандаш;
  • — циркуль;
  • — линейка;
  • — угольник;
  • — кусок тонкой проволоки;
  • — ножницы;
  • — клей.

Инструкция

  • Начните работу с черчения центрального правильного пятиугольника. Для этого начертите циркулем окружность. Проведите через ее центр диаметр. Теперь его необходимо разделить на три части. Существует теорема, доказывающая, что трисекция (то есть, разделение отрезка или угла на три одинаковые части) при помощи линейки без делений и циркуля невозможна. Поэтому либо измерьте диаметр линейкой и поделите его на три, а затем отметьте на нем соответствующие точки по делениями линейки, либо измерьте его куском тонкой проволоки, сложите ее втрое, затем распрямите, наложите на диаметр и отметьте точки в местах сгиба.
  • В результате деления диаметра на три части на нем получатся две точки. Через одну из них проведите к диаметру при помощи угольника перепендикуляр. Он пересечет окружность в двух местах. Из каждого из них проведите по лучу, проходящему через вторую точку на диаметре. Они пересекут окружность еще в двух местах, ну а пятое место пересечения образует сам диаметр. Останется лишь соединить их между собой, и получится правильный пятиугольник, вписанный в окружность.
  • Начертите тем же способом еще одиннадцать пятиугольников, расположив их таким образом, чтобы получилась фигура, подобная показанной на рисунке. Пририсуйте к ее граням сбоку небольшие лепестки, облегчающие склейку. Затем вырежьте ее и склейте. То, что должно получиться в результате, показано на иллюстрации в заголовке статьи.
  • Поскольку у додекаэдра ровно двенадцать граней, в виде этой фигуры можно изготавливать объемные, устойчивые настольные календари. Для этого сначала составьте на каждой из граней по календарю на один месяц, и лишь затем вырежьте и склейте фигуру. Также такой календарь можно сгенерировать автоматически, перейдя по указанной ниже ссылке. Год определится автоматически по встроенным часам сервера, а язык названий месяцев и дней недели — по настройкам вашего браузера.

Вам понадобится

  • — плотная бумага;
  • — карандаш;
  • — циркуль;
  • — линейка;
  • — угольник;
  • — кусок тонкой проволоки;
  • — ножницы;
  • — клей.

Инструкция

Начните работу с черчения центрального . Для этого начертите циркулем окружность. Проведите через ее центр диаметр. Теперь его необходимо разделить на три части. Существует теорема, доказывающая, что трисекция (то есть, разделение отрезка или угла на три ) при помощи линейки без делений и циркуля . Поэтому либо измерьте диаметр линейкой и поделите его на три, а затем отметьте на нем соответствующие точки по делениями линейки, либо измерьте его куском тонкой , сложите ее втрое, затем распрямите, наложите на диаметр и отметьте точки в местах сгиба.

В результате деления диаметра на три части на нем получатся две точки. Через одну из них проведите к диаметру при помощи угольника перепендикуляр. Он пересечет окружность в двух местах. Из каждого из них проведите по лучу, проходящему через вторую точку на диаметре. Они пересекут окружность еще в двух местах, ну а пятое место пересечения образует сам диаметр. Останется лишь соединить их между собой, и получится правильный , вписанный в окружность.

Начертите тем же способом еще одиннадцать пятиугольников, расположив их таким образом, чтобы получилась фигура, подобная показанной на рисунке. Пририсуйте к ее граням сбоку небольшие лепестки, облегчающие склейку. Затем вырежьте ее и склейте. То, что должно получиться в результате, показано на иллюстрации в заголовке статьи.

Поскольку у додекаэдра ровно двенадцать граней, в виде этой фигуры можно изготавливать объемные, устойчивые настольные календари. Для этого сначала составьте на каждой из граней по календарю на один месяц, и лишь затем вырежьте и склейте фигуру. Также такой календарь можно сгенерировать автоматически, перейдя по указанной ниже ссылке. Год определится автоматически по встроенным часам сервера, а язык названий месяцев и дней недели — по настройкам вашего браузера.

Источники:

  • Генератор календарей в виде додекаэдра
  • как сделать правильный додекаэдр

Стереометрия, как часть геометрии, гораздо ярче и интереснее именно тем, что фигуры здесь не плоскостные, а объемные. В многочисленных задачах требуется рассчитать параметры параллелепипедов, конусов, пирамид и других трехмерных фигур. Иногда уже на этапе построения возникают сложности, которые легко устраняются, если следовать простым принципам стереометрии.

Вам понадобится

  • — линейка;
  • — карандаш;
  • — циркуль;
  • — транспортир.

Инструкция

Определитесь с количеством граней, а также количеством углов в многоугольниках самих граней перед . Если в условии говорится о правильном многограннике, то стройте его так, чтобы он был выпуклый (не ломанный), чтобы грани представляли собой правильные многоугольники, а в каждой вершине трехмерной фигуры сходилось одинаковое количество ребер.

Помните об особых многогранниках, для которых есть постоянные характеристики:
— тетраэдр состоит из треугольников, имеет 4 вершины, 6 ребер, сходящихся в вершинах по 3, а также 4 грани;
— гесаэдр, или куб, состоит из квадратов, имеет 8 вершин, 12 ребер, сходящихся по по 3 на вершинах, а также ;
— октаэдр состоит из треугольников, имеет 6 вершин, 12 ребер, примыкающих по 4 к вершинам, а также 8 граней;
— – это двенадцатигранная фигура, состоящая из пятиугольников, имеющая 20 вершин, а также 30 ребер, примыкающих к вершине по 3;
— , в свою очередь, имеет 20 треугольных граней, 30 ребер, примыкающих по 5 к каждой из 12 вершин.

Начните построение с параллельных прямых, если ребра многогранника параллельны. Это касается параллелепипеда,

Додекаэдр — очень необычная объемная фигура, состоящая из 12 одинаковых граней, каждая из которых представляет собой Чтобы собрать додекаэдр своими руками, вовсе не обязательно обладать особыми навыками с этой задачей справится даже ребенок. Немного сноровки, и у вас обязательно все получится!

Необходимые материалы и инструменты

  • Лист белой и цветной бумаги. Оптимальная плотность — 220 г/м 2 . Очень тонкая бумага слишком сильно мнется при сборке, а очень толстый картон изламывается на сгибах.
  • Развертка додекаэдра (шаблон).
  • Тонкий или очень острые ножницы.
  • Простой карандаш или маркер.
  • Транспортир.
  • Длинная линейка.
  • Жидкий клей.
  • Кисточка.

Инструкция

  1. Если у вас есть принтер, то можно распечатать шаблон сразу на листе, но его вполне можно начертить самостоятельно. Пятиугольники строятся с помощью транспортира и линейки, угол между соседними линиями должен составлять ровно 108 о, подбирая длину грани можно сделать большой или маленький додекаэдр. Развертка представляет собой 2 соединенных «цветка», состоящих из 6 фигур. Обязательно оставьте небольшие припуски, они нужны для склеивания.
  2. Аккуратно вырежьте заготовку ножницами или ножом на специальном чтобы не повредить поверхность стола. Далее пройдитесь по местам сгибов острым углом линейки, это заметно облегчит сборку фигуры и сделает грани более аккуратными.
  3. С помощью кисточки нанесите на припуски немного клея и соберите фигуру подгибая края внутрь. Если вы решили сделать додекаэдр своими руками, а под рукой не оказалось даже скотча, вырежьте припуски одной половины шаблона в виде удлиненных треугольников, а на сгибах второй части сделайте небольшие разрезы. Затем просто вставьте краешки в пазы, и конструкция будет довольно прочно держаться.

Готовую фигуру можно разрисовать или украсить наклейками. Модель большого размера можно превратить в оригинальный календарь, ведь количество сторон соответствует количеству месяцев в году. Если вы увлекаетесь японским можно сделать додекаэдр своими руками в технике модульного оригами.

  1. Подготовьте 30 листов обычной офисной бумаги. Хорошо если они будут цветными и двухсторонними, можно выбрать несколько оттенков.
  2. Изготовление модулей. Мысленно расчертите лист на четыре одинаковые полоски и сложите гармошкой. Загните углы в на одну сторону в противоположных направлениях, получившаяся фигура должна напоминать параллелограмм. Осталось перегнуть заготовку по короткой диагонали. Сделайте 30 модулей и приступайте к сборке.
  3. Додекаэдр имеет 10 узлов, каждый собирается из трех элементов. Подготовьте все части и вложите их друг в друга. Чтобы модули не разъезжались, фиксируйте стыки скрепками, когда вы полностью соберете фигуру, их можно будет убрать.

Когда только вы освоите понравившуюся вам технику, можно научить собирать додекаэдр своими руками вашего ребенка или товарища. Ведь изготовление объемных фигур не только хорошо развивает моторику пальцев, но и формирует пространственное воображение.

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Развивающие и обучающие пособия в интернет-магазине «Интеграл»
Тренажер по Моро М.И. Тренажер по Петерсон Л.Г.

Из истории додекаэдра

Каждый, кто учился в школе, изучал геометрию, кто-то ее любил, а кто-то не очень, а кому-то только предстоит познакомиться с этой наукой. И, конечно же, всем задавали нарисовать или собрать различные геометрические фигуры, а потом оценивали лучшую работу. Но, к сожалению не все учителя рассказывают о происхождении геометрических фигур, для чего они нужны, какое значение имеют и где применяются. А у фигур очень богатая история, они важны так же, как и любые открытия в нашем мире. А встречаются они повсюду, просто мы не всегда их замечаем. Сегодня мы расскажем вам о додекаэдре.

Слово додекаэдр имеет греческое происхождение и состоит из 2 слов: dodeka (двенадцать) и hedra (грань). Додекаэдр имеет 12 граней, 20 вершин, в каждой из которых сходиться 3 ребра и 30 рёбер. Сумма плоских углов равна 324°. Это двенадцатигранник, который составлен из двенадцати правильных пятиугольников. Додекаэдр правильный многогранник, он имеет три звездчатые формы.

О додекаэдре было известно уже в древние времена. Например, ученикам Пифагорейской школы запрещалось произносить это слово за пределами школы, так как за это они могли лишиться жизни. К этой фигуре относились как к святой фигуре, о ней даже боялись что-либо сказать. Лишь спустя двести лет, во времена Платона, об этой фигуре начали очень осторожно говорить. Запрещено было произносить что-то лишнее, тем более оскорбительное или пренебрежительное. Верили в то, что додекаэдр находится в энергетическом поле людей и является высшей формой сознания человека. К тому же считалось, что люди живут внутри огромного додекаэдра, в котором расположена наша вселенная и когда ум человека достигает самого предела пространства Космоса, он натыкается на додекаэдр, замкнутый в сфере.

Додекаэдр в нашей жизни

Где же можно встретить додекаэдр? Подумайте хорошенько! Наверное почти все видели его в качестве генератора случайных чисел, например, по телевизору в игре лото или в настольных ролевых играх. Додекаэдр можно встретить в игре «Пентакор», мир которого представлен в виде этой фигуры. И, конечно же все слышали про Пентагон, это здание Министерства обороны США имеет форму правильного пятиугольника.

В августе 2006 года при нанесении на карты распределения тёмной материи в скоплении галактик, были сделаны выводы, что наша Вселенная выглядит как набор бесконечно повторяющихся додекаэдров.

Правильные многогранники всегда привлекали совершенством своих форм, полной, казалось бы, невозможной симметричностью. Некоторые из таких тел встречаются в природе, например в виде кристаллов, другие — могут быть в виде вирусов или простейших микроорганизмов.

Собрать эту удивительную фигуру вы можете, используя наши развертки додекаэдра.

Развертка додекаэдра из бумаги или из картона

Схема правильного додекаэдраСхема додекаэдра с формуламиСхема додекаэдра с великими открытиями человечества

Додекаэдром называется правильный многогранник, составленный из двенадцати правильных пятиугольников. Эта эффектная объемная фигура обладает центром симметрии, называемым центром додекаэдра. Кроме того, в ней присутствуют пятнадцать плоскостей симметрии (в каждой грани любая из них проходит через середину противоположного ребра и вершину) и пятнадцать осей симметрии (пересекающих середины параллельных противолежащих ребер). Каждая из вершин додекаэдра является вершиной трех пятиугольников правильной формы.

Свое название конструкция получила по количеству входящих в нее граней (традиционно древние греки давали многогранникам имена, отображающие число граней, составляющих структуру фигуры). Таким образом, понятие «додекаэдр» образовано из значений двух слов: «додека» (двенадцать) и «хедра» (грань). Фигура относится к одному из пяти Платоновых тел (наряду с тетраэдром, октаэдром, гексаэдром (кубом) и ). Интересно, что согласно многочисленным историческим документам, все они активно использовались жителями Древней Греции в виде настольных игральных костей и изготавливались из самого различного материала.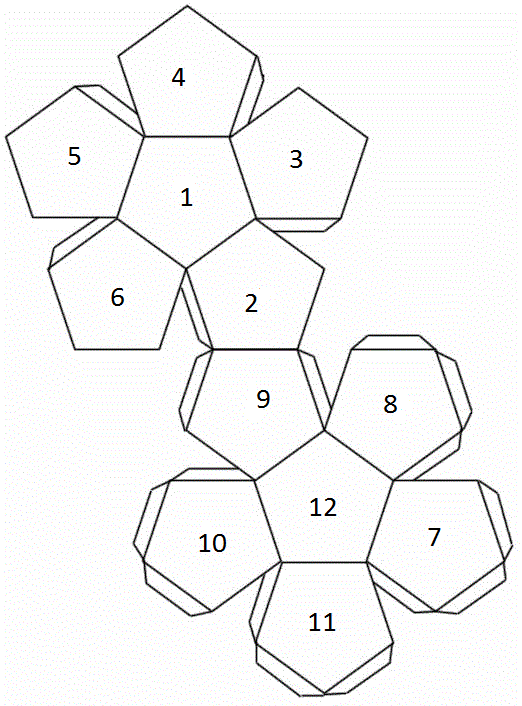

Правильные многогранники всегда привлекали людей своей красотой, органичностью и необыкновенным совершенством форм, но додекаэдр имеет особую историю, которая из года в год обрастает все новыми, иногда совершенно мистическими, фактами. Представители многих цивилизаций усматривали в нем сверхъестественную и таинственную сущность, утверждая, что: «Из числа двенадцать произрастает многое». На территориях древних разрушенных государств до сих пор находят маленькие фигурки в виде додекаэдров, выполненные из бронзы, камня или кости. Кроме того, при раскопках на землях современной Англии, Франции, Германии, Венгрии, Италии археологи обнаружили несколько сотен так называемых «римских додекаэдров», датирующихся II-III-м веками нашей эры. Основные размеры фигурок составляют от четырех до одиннадцати сантиметров, причем отличаются они самыми невероятными узорами, текстурами и техникой исполнения. Выдвинутая еще во времена Платона версия о том, что Вселенная представляет собой огромного размера додекаэдр, нашла подтверждение уже в начале XXI -го века.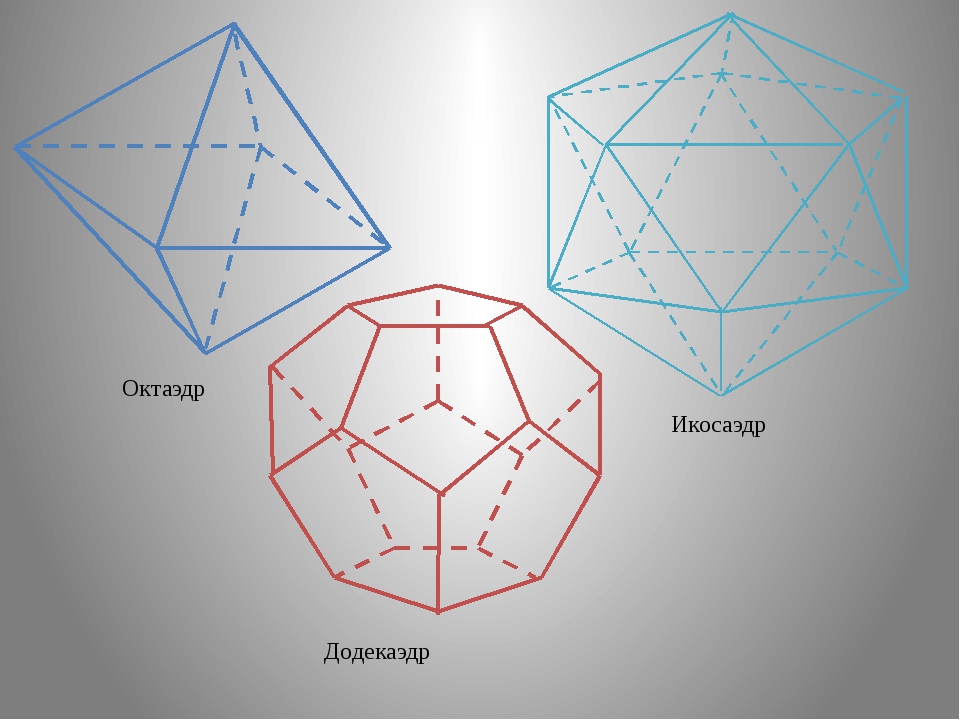 После тщательного анализа данных, полученных при помощи WMAP(многофункционального космического аппарата NASA), ученые согласились с предположением древнегреческих астрономов, математиков и физиков, в свое время занимавшихся вопросами изучения небесной сферы и ее строением. Более того, современные исследователи считают, что наша Вселенная представляет собой бесконечно повторяющийся набор додекаэдров.

Как сделать правильный додекаэдр своими руками

Сегодня конструкция данной фигуры нашла свое отображение во многих вариантах художественного творчества, архитектуре и строительстве. Народные умельцы изготавливают из цветной или белой бумаги необыкновенные по красоте оригами в виде ажурных додекаэдров, а из картона делают оригинальные и прочее). В продаже можно приобрести уже готовые наборы, содержащие все необходимое для изготовления сувениров, но наиболее интересно произвести весь процесс работы своими руками, начиная от построения отдельных деталей и заканчивая сборкой готовой конструкции.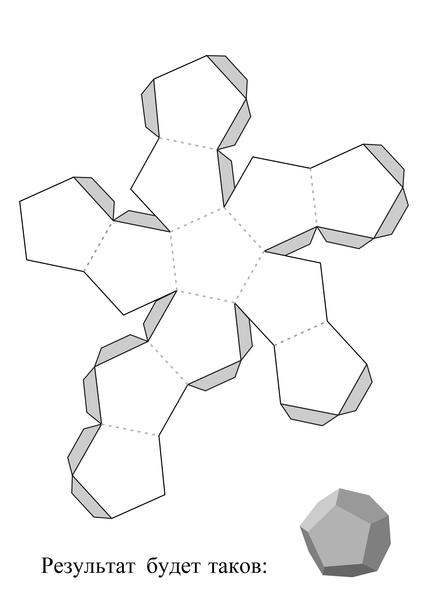

Материалы:

Для того, чтобы сделать правильный додекаэдр из картона, необходим собственно сам материал и подручные средства:

  • ножницы,
  • карандаш,
  • ластик,
  • линейка,
  • клей.

Хорошо иметь тупой нож или какое-либо приспособление для загибания припусков, но если их нет, то вполне подойдет металлическая линейка или те же ножницы.

Как сделать звездчатый додекаэдр

Звездчатые додекаэдры имеют более сложную конструкцию по сравнению с обычными. Эти многогранники подразделяются на малый (первого продолжения), средний (второго продолжения) и большой (последняя звездчатая форма правильного додекаэдра). Каждый из них отличается своими особенностями построения и сборкой. Для работы Вам потребуются те же материалы и инструменты, что и для изготовления стандартного додекаэдра. Если Вы решили сделать первый вариант (малый додекаэдр), то необходимо построить чертеж первого элемента, который станет основой для всей конструкции (в дальнейшем производится ее склеивание или сборка деталей при помощи скрепок).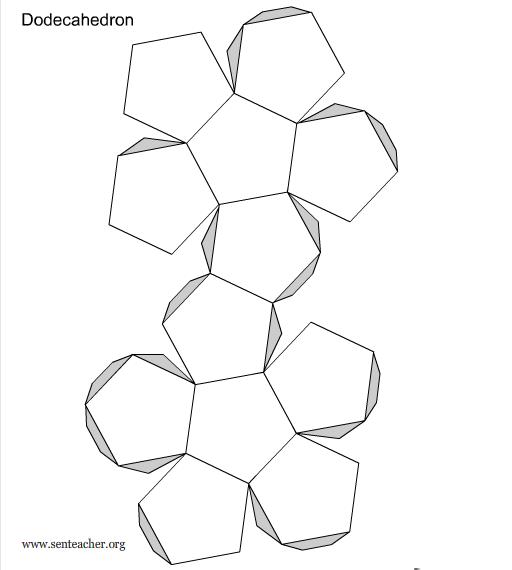

Зачем в древности был нужен и как использовался «Римский додекаэдр». | Статьи

Римский додекаэдр – загадочный, таинственный предмет. Он начал использоваться в Европе с приходом туда римлян в I веке до нашей эры, а потом был забыт навсегда.

Его назначение ученые не могли раскрыть сотни лет.

«…Есть много людей, которые трудятся над тем, чтобы разрешить разные вопросы, а когда они разрешены, то оказывается. Что они и гроша ломанного не стоят».

(«Дон Кихот», Мигель Сервантес).

«Римские додекаэдры» были найдены археологами во множественном числе на территории стран современной Западной Европы (Франции, Великобритании, Бельгии, Германии, Швейцарии, Голландии, Италии и других).

Время изготовления найденных додекаэдров относят к I — IV векам нашей эры. В основном они были сделаны из бронзы, реже из свинца и из камня. В музеях и запасных фондах, перечисленных стран хранится более сотни таких предметов.

Есть также монолитные камни-додекаэдры с закругленными гранями без отверстий, есть с треугольными гранями икосаэдры (без отверстий). Они имели каждый своё предназначение. Речь в данном материале не о них.

На карте Европы отмечено, где нашли додекаэдры.

Археологи находили додекаэдры в разных местах: в захоронениях людей, в кладах монет, четыре штуки нашли на развалинах римской дачи, один в Помпеях (Италия) в шкатулке с женскими украшениями, магическими предметами и прочее.

О чём говорят места находок? – Что предметами пользовались в помещениях. Они были необходимыми принадлежностями личного (семейного) употребления и, судя по

различным внешним украшениями на них (отделкой серебром) выполняли декоративную функцию. Примерно, как в наши дни на ручках столовых приборов (ложек, вилок, ножей) делают простейшие незамысловатые узоры, которые не имеют практического назначения.

Додекаэдры были размером от 4 -11 см полые внутри, изготовлены из бронзы.

В центре двенадцати граней были отверстия различного диаметра, расположенные безо всякой строго установленной для всех закономерности.

Предназначение их было на многие века забыто. В исторических описаниях о нём не было упомянуто, вероятно потому, что особо важного предназначения у него не было.

Новые археологические находки в XX – XXI веке нисколько не приоткрыли тайну завесы и не дали ключа к разгадке древнего римского додекаэдра.

Ученые выдвинули множество гипотез, придумывались: мистические, геодезические, военные, астрономические, математические, сельскохозяйственные версии, то их называли священными предметами пифагорейцев, то культовыми предметами друидов, элементами материи, то чуть ли не форма мироздания, позже подключились ученые с идеями молекулярного устройства и так далее… Всё, что придумано было собрано в «одну кучу» и в результате ничего не получилось.

В Википедии перечислены некоторые предположения, как додекаэдры могли быть использованы, например: игральные кости, инструмент для калибровки труб, элемент армейского штандарта, дальномер, элемент для вязания, детская игрушка (современный спиннер). Некоторые ученые говорили, что додекаэдры символизировали огонь.

Наиболее близкую к действительности версию высказали в 1907 году, заявив, что это подсвечник, круглую свечу де ставили в отверстие, чтобы она в нём лучше держалась, так как внутри одного додекаэдра был найден воск. Но все эти версии не имели сколько-нибудь существенного смыслового объяснения.

Тогда, что же это такое и каково было предназначение додекаэдра?

То, что внутри додекаэдра был найден воск послужит «ниточкой», чтобы размотать «таинственный клубок» исторической загадки.

Начнём с утверждения учёных о том, что первые свечи были придуманы в Древнем Египте ещё III тысячи лет до нашей эры. Делали их из растения ситника, а фитиль из сердцевины высушенного тростника вымоченного в животном жире. После этого пять тысяч лет шло усовершенствование свеч. Впоследствии для их изготовления стали использовать пчелиный воск. Для его большей пластичности при изготовлении свечей к расплавленному воску могли добавлять растительные или животные жиры.

Какие свечи есть в настоящее время знают все и когда-нибудь ими пользовались.

В древние времена в долгие тёмные вечера свечами освещали помещения, палатки. Расход свечей был большой. Свечи стоили дорого и не все люди имели возможность ими пользоваться ежедневно.

Для изготовления свечей и их практичного использования люди прикладывали ум – как сделать, чтобы управлять горением свечи, чтобы она лучше и дольше светила?

Малого диаметра свечи быстро сгорают и для долгого освещения не годились. Поэтому делали толстые. Толстая свеча горит дольше, но у неё есть один недостаток — по мере горения фитиль с огнём опускается внутрь свечи, стенки её не успевают плавиться и она не дает света. Чтобы фитиль дольше не обугливался, его надо постоянно смачивать жиром (воском). Чтобы толстая свеча долго горела и при этом пламя фитиля не опускалось во внутрь, нужно было равномерно плавить толстую свечу по краям, чтобы расплавленный жир (воск) от краев свечи постоянно стекал к её центру. — Для этого и был придуман древними изобретателями «римский додекаэдр».

Судя по размерам найденных додекаэдров, древние свечи были также от 4 — 11 см.

И возможно, что свечи были не всегда в сечении круглые, как сейчас (хотя круг для плавления свечи идеальная расходная форма). Свечи могли быть и пятигранные (фигура близкая к кругу). Но для додекаэдра это не столь важно, так как он мог быть использован одинаково полезно на круглой и пятигранной свече.

Додекаэдр использовали, ставя его на горящую свечу — сверху.

Додекаэдры были разных размеров и применяли их в зависимости от толщины используемых свеч. Чем толще была свеча, тем крупнее использовался додекаэдр.

Свечи были разного размера в поперечнике и фитили (от толщины) тоже были разного диаметра. Поэтому в гранях додекаэдра отверстия были разного диаметра, чтобы сделать его максимально универсальным для свечей многих размеров.

По мере горения свечи, для удлинения её срока пользования, додекаэдр много раз за вечер переворачивали, ставя попеременно на свечу гранями с отверстиями разного диаметра, опять же для равномерности плавления воска.

Ближе к фитилю металл додекаэдра был горячее и воск под ним плавился быстрее, стекая в «кратер» к центру, а дальше от фитиля металл был холоднее и воск под ним плавился медленнее. Равномерное плавление свечи позволяло увеличить время горения, способствовало её полному сгоранию, не позволяло воску стекать наружу по краям (как происходит с тонкими свечами).

Кроме того, додекаэдр защищал пламя свечи от ветра, так как каждый раз разжигать потухший огонь, в те времена было не просто.

Помимо всего, свет через круглые отверстия в гранях служил «декоративному» освещению помещения. Свечи и додекаэдр был всегда на видном месте, поэтому богатые люди, чтобы показать своё состоятельное положение иногда его украшали серебром. Например, в окрестностях Женевы в Швейцарии был найден маленький литой свинцовый додекаэдр с гранями 15 миллиметров, покрытый снаружи пластинками из серебра с латинскими зодиакальными знаками. То, что он был маленький по размеру, серебряный и украшенный знаками, говорит, что его владелец был богатый человек и позволял себе пользоваться тонкими, быстро сгорающими, дорогими свечами.

Психология людей не меняется со временем и в наше время стараются обустроить свой быт, используя приукрашенные бытовые вещи – тоже делали и раньше.

Додекаэдр, находясь на свече, от пламени фитиля становился горячим.

Потому, чтобы его можно было брать голыми руками и переворачивать – на вершинах додекаэдра (не всегда, но часто) были сделаны шарики, которые нагреваются меньше. Это своего рода полезное дополнение к световому прибору.

Додекаэдр был не очень легким, вес его был достаточным, чтобы нагреваясь, плавить воск толстой свечи. Меняя диаметр отверстий, поставленных на свечу, можно было регулировать высоту горящего фитиля и таким образом, освещенность помещения.

Например, если поставить додекаэдр на свечу маленьким отверстием, то фитиль и пламя свечи будет маленьким. Свеча будет медленнее гореть и меньше давать света, так как расплавленный воск будет, напирая, топить фитиль, не давая ему разгореться.

Меньший диаметр отверстия ставился на свечу, а на противоположной грани для выхода пламени было отверстие большего диаметра – это позволяло додекаэдру не так сильно разогреваться. Если на свечу ставилась грань с большим отверстием, то свеча будет гореть быстрее, так как пламя фитиля будет больше и выше. Размером отверстия регулировали высоту пламени фитиля (то есть освещенность) и время горения свечи.

В общем и целом этот не хитрый предмет имел много полезных свойств.

В старейшем городе Тонгерен в Бельгии, известном ещё в I веке до нашей эры, так были взволнованы и озадачены тайной «римского додекаэдра», что сделали ему памятник.

В музее города Тонгерен есть (найденный там в 1937 году за стенами древнего города), додекаэдр: материал бронза, высота без шариков — 66 мм., с шариками — 81 мм., вес – 172 грамма. Диаметр отверстий (по парам) на противоположных гранях: 10,6 — 13,0; 13,8 — 14,0; 15,6 — 17,8; 20,3 – 20,5; 23,0 -26,3; 25,2 – 27,0 мм. — размеры музейного образца.

Памятник додекаэдру в городе Тонгерен в Бельгии

Каменный «римский додекаэдр».

Бронзовый «Римский додекаэдр» в музее города Тонгерен в Бельгии.

На бронзовом бельгийским додекаэдре нет никаких концентрических окружностей, нет и рисунков на гранях, и это нисколько не мешало ему выполнять свою функцию.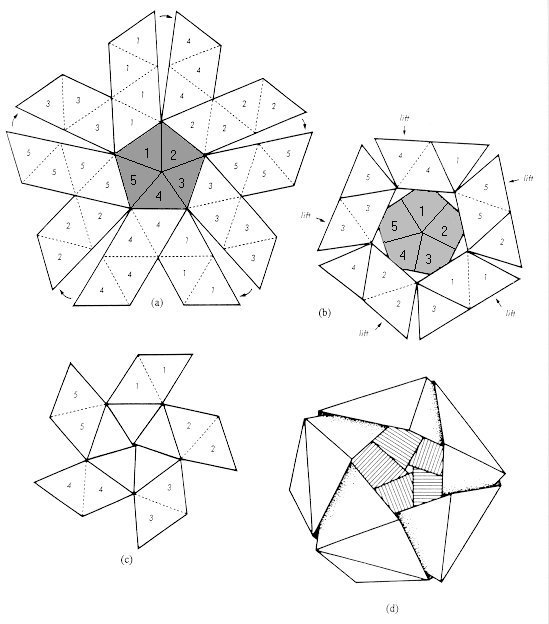

Концентрические окружности на гранях додекаэдра помогали мастеру ровно изготовить пятиугольные пластины (с одинаковыми по длине гранями), для последующего их плотного соединения, безошибочно его собрать, чтобы на гранях попарно были отверстия разного диаметра, а при его использовании — окружности помогали легче ориентироваться какой гранью поставить.

Додекаэдры изготовлялись разными мастерами, в разное время, в разных странах, поэтому имели несущественные внешние отличия. Например, чтобы приукрасить предмет, иногда мастера на гранях изображали маленькие кружочки с точкой в центре. Кружок с точкой в центре это древний символ Солнца – то есть в переносном смысле: свет, яркость, освещенность.

Способствовать равномерному плавлению толстой свечи мог бы и полый куб, но у него мало рабочих граней, поэтому большое пространство оставалось затемнённым, нет отверстий для выхода света вниз, необходимых для чтения и письма под свечой.

К тому же у более практичного (в данном случае) додекаэдра за счёт большего числа граней — больше возможности для регулирования процесса горения. Ну, а форма додекаэдра, близкая к шару, взята из геометрии древних египтян и греков.

Додекаэдр был далеким предшественником керосиновой лампы, функции которого в лампе преобразились — пламя фитиля закрывалось от дождя и ветра стеклом, а яркость пламени и освещенность регулировалась вручную, вращением колёсика, изменяющего высоту выдвижения фитиля для горения.

Со временем с развитием человечества потребность в додекаэдрах отпала. Люди стали больше заниматься пчеловодством, воска стало много больше. Дороговизна свечей прошла и постепенно потребность в додекаэдрах отпала. Точно так же как отпала потребность и в керосиновой лампе, как и во множестве других предметах древнего, средневекового и более позднего быта людей.

Упоминается иногда вместе с римскими и вьетнамские золотые додекаэдры, но они имеют совсем другой вид, целостную или полую форму и много отличий от римских.

Вот, в принципе и весь секрет «римского додекаэдра».

Хотя, Мигель Сервантес и говорил, что зачастую разгадка исторической тайны «гроша ломаного» не стоит, но древним жителям Европы додекаэдр приносил немалую пользу, так как в какой-то мере улучшал их быт, экономил воск, денежные ресурсы на покупку свечей для освещения помещений в долгие тёмные вечера и ночи.

В наше время изобретатели тоже постоянно «ломают головы», придумывая бессчетное число энергосберегающих технологий, предметов бытового и промышленного назначения практически во всех сферах жизни.

Владимир Гарматюк

Россия, г. Вологда

16.11.2020

как сделать додекаэдр из бумаги

Додекаэдр — очень необычная объемная фигура, состоящая из 12 одинаковых граней, каждая из которых представляет собой Чтобы собрать додекаэдр своими руками, вовсе не обязательно обладать особыми навыками с этой задачей справится даже ребенок. Немного сноровки, и у вас обязательно все получится!

Необходимые материалы и инструменты

  • Лист белой и цветной бумаги. Оптимальная плотность — 220 г/м 2 . Очень тонкая бумага слишком сильно мнется при сборке, а очень толстый картон изламывается на сгибах.
  • Развертка додекаэдра (шаблон).
  • Тонкий или очень острые ножницы.
  • Простой карандаш или маркер.
  • Транспортир.
  • Длинная линейка.
  • Жидкий клей.
  • Кисточка.

Инструкция

  1. Если у вас есть принтер, то можно распечатать шаблон сразу на листе, но его вполне можно начертить самостоятельно. Пятиугольники строятся с помощью транспортира и линейки, угол между соседними линиями должен составлять ровно 108 о, подбирая длину грани можно сделать большой или маленький додекаэдр. Развертка представляет собой 2 соединенных «цветка», состоящих из 6 фигур. Обязательно оставьте небольшие припуски, они нужны для склеивания.
  2. Аккуратно вырежьте заготовку ножницами или ножом на специальном чтобы не повредить поверхность стола. Далее пройдитесь по местам сгибов острым углом линейки, это заметно облегчит сборку фигуры и сделает грани более аккуратными.
  3. С помощью кисточки нанесите на припуски немного клея и соберите фигуру подгибая края внутрь. Если вы решили сделать додекаэдр своими руками, а под рукой не оказалось даже скотча, вырежьте припуски одной половины шаблона в виде удлиненных треугольников, а на сгибах второй части сделайте небольшие разрезы. Затем просто вставьте краешки в пазы, и конструкция будет довольно прочно держаться.

Готовую фигуру можно разрисовать или украсить наклейками. Модель большого размера можно превратить в оригинальный календарь, ведь количество сторон соответствует количеству месяцев в году. Если вы увлекаетесь японским можно сделать додекаэдр своими руками в технике модульного оригами.

  1. Подготовьте 30 листов обычной офисной бумаги. Хорошо если они будут цветными и двухсторонними, можно выбрать несколько оттенков.
  2. Изготовление модулей. Мысленно расчертите лист на четыре одинаковые полоски и сложите гармошкой. Загните углы в на одну сторону в противоположных направлениях, получившаяся фигура должна напоминать параллелограмм. Осталось перегнуть заготовку по короткой диагонали. Сделайте 30 модулей и приступайте к сборке.
  3. Додекаэдр имеет 10 узлов, каждый собирается из трех элементов. Подготовьте все части и вложите их друг в друга. Чтобы модули не разъезжались, фиксируйте стыки скрепками, когда вы полностью соберете фигуру, их можно будет убрать.

Когда только вы освоите понравившуюся вам технику, можно научить собирать додекаэдр своими руками вашего ребенка или товарища. Ведь изготовление объемных фигур не только хорошо развивает моторику пальцев, но и формирует пространственное воображение.

ИКОСАЭДР

РАЗВЕРТКА ИКОСАЭДРА. Развертка состоит из двадцати правильных треугольников, кроме того, развертка включает в себя еще и клапаны.

КАК СДЕЛАТЬ ИКОСАЭДР ПО РАЗВЕРТКЕ. Согнуть развертку по всем необходимым линиям «горой». Если развертка выполнена на плотной бумаге, то по всем линиям сгиба провести по изнанке острым краем ножниц.

КАК СКЛЕИТЬ ИКОСАЭДР? После того, как развертка согнута, промажьте клапаны клеем (лучше использовать ПВА), и склейте 20-сторонний шар.

ДРУГОЙ СПОСОБ СКЛЕЙКИ ИКОСАЭДРА.

Из бумаги вырезается 20 отдельных кругов, в которые вписаны правильные треугольники.

Сгибаем заготовленные круги по граням треугольника и склеиваем. Причем — по желанию: гранями наружу или гранями вовнутрь.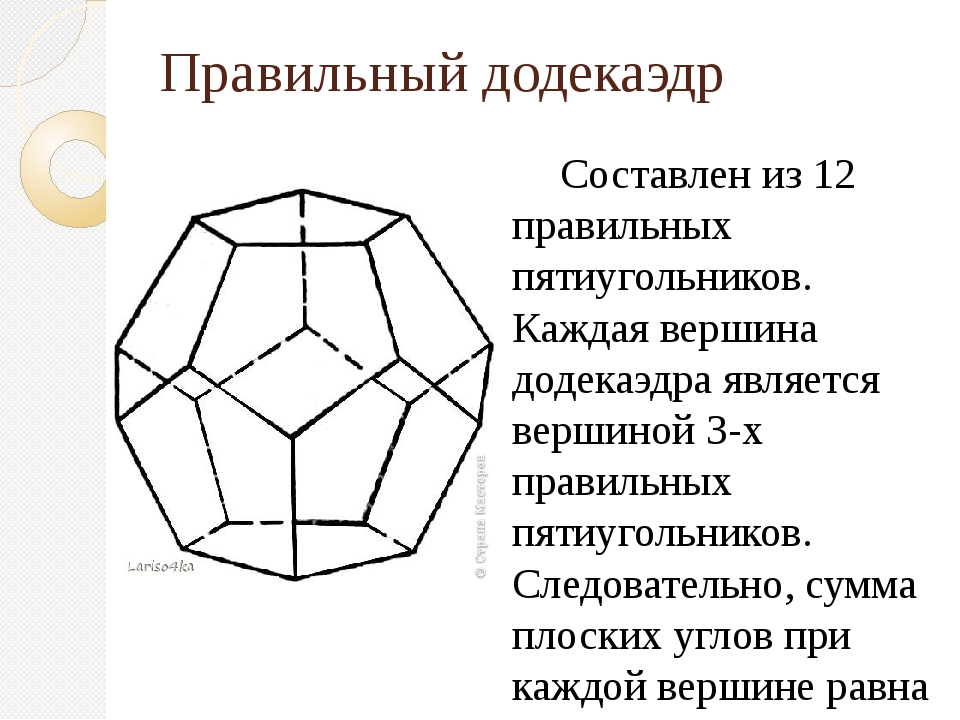

Икосаэдр — г Змеиногорск Алтай

ГЕРАЛЬДИКА.

Шар Икосаэдра на гербе г.Змеиногорска, Алтай.

НАЗВАНИЕ. Звезда Кеплера или Двойной тетраэдр.

РАЗВЕРТКА ЗВЕЗДЧАТОГО ОКТАЭДРА. Развертка состоит из 24-ех правильных тре-угольников, кроме того, развертка включает в себя еще и клапаны.

КАК СДЕЛАТЬ ЗВЕЗДЧАТЫЙ ОКТАЭДР ПО РАЗВЕРТКЕ. Согнуть развертку по всем необходимым линиям. Если развертка выполнена на плотной бумаге, то по всем линиям сгиба провести по изнанке острым краем ножниц. Если хотите получить двухцветный тетраэдр, то раскрасьте треугольнички, отмеченные точками, другим цветом.

Вариант развертки

фото Наты

ВНЕШНИЙ ВИД. Звездный октаэдр представляет собой конгломерат из двух правильных тетраэдров.

Posted in |

РАЗВЕРТКА ДОДЕКАЭДРА

ДОДЕКАЭДР — один из пяти правильных многогранников, так называемое Платоновское тело.

НАЗВАНИЕ. В переводе «додекаэдр» значит — «12 граней

В ЧИСЛОВОМ ВЫРАЖЕНИИ. Додекаэдр имеет 12 граней, 20 вершин, 30 ребер.

РАЗВЕРТКА ДОДЕКАЭДРА. Развертка состоит из двенадцати правильных пяти-угольников, кроме того, развертка включает в себя еще и клапаны.

КАК СДЕЛАТЬ ДОДЕКАЭДР ПО РАЗВЕРТКЕ. Согнуть развертку по всем необходимым линиям «горой». Если развертка выполнена на плотной бумаге, то по всем линиям сгиба провести по изнанке острым краем ножниц.

ПРОСТРАНСТВЕННОЕ ПОСТРОЕНИЕ. В каждой вершине додекаэдра сходится три пяти-угольника

СТИХИИ. По мнению некоторых средневековых ученых, додекаэдру соответствует Эфир (то есть пустота)

Пожалуй, самый древний предмет в форме додекаэдра был найден в северной Италии, около Падуи, в конце XIX века, он датируется 500 г. до н. э. и предположительно использовался этрусками в качестве игральной кости.

Додекаэдр рассматривали в своих сочинениях древнегреческие учёные. Платон сопоставлял с правильными многогранниками различные классические стихии. О додекаэдре Платон писал, что «…его бог определил для Вселенной и прибегнул к нему в качестве образца»

В 2003 году, при анализе данных космического аппарата WMAP, была выдвинута гипотеза, что Вселенная представляет собой додекаэдрическое пространство Пуанкаре

На территории нескольких европейских стран найдено множество предметов, называемых римскими додекаэдрами, относящихся ко II-III вв. н. э., назначение которых не совсем понятно.

Древние мудрецы говорили: «Чтобы познать невидимое, смотри внимательно на видимое». В плане сакральных сил додекаэдр самый мощный многогранник. Не зря Сальвадор Дали для своей «Тайной вечере» выбрал эту фигуру. В ней от двенадацати пятиугольников — тоже сильной фигуре, силы концентрируются в одной точке — на Иисусе Христе.

А теперь взгляните да додекаэдр и осознайте, что число 5 формирует КРИСТАЛЛ СИЛЫ.

Фигура относится к одному из пяти Платоновых тел (наряду с тетраэдром, октаэдром, гексаэдром (кубом) и икосаэдром). Интересно, что согласно многочисленным историческим документам, все они активно использовались жителями Древней Греции в виде настольных игральных костей и изготавливались из самого различного материала.

ДОДЕКАЭДР В ПРИРОДЕ. Кристалл пирита — сернистого колчедана — FeS2 — очень красив, и, по легенде, именно он подсказал грекам идею «правильного» додекаэдра.

Если длину ребра додекаэдра принять за , то площадь всей поверхности додекаэдра равна

Радиус сферы, описанной вокруг дадекаэдра, рассчитывается следующим образом:

Расчет радиуса сферы, вписанной в додекаэдр можно сделать так:

Додекаэдр — очень необыкновенная большая фигура, состоящая из 12 схожих граней, любая из которых представляет собой верный пятиугольник. Чтоб собрать додекаэдр своими руками, совсем не непременно владеть особенными способностями 3D моделирования, с этой задачей управится даже ребенок. Незначительно сноровки, и у вас непременно все получится!

Нужные материалы и инструменты

  • Лист белоснежной и цветной бумаги. Лучшая плотность — 220 г/м 2 . Очень узкая бумага очень очень мнется при сборке, а очень толстый картон изламывается на сгибах.
  • Развертка додекаэдра (шаблон).
  • Узкий канцелярский ножик либо очень острые ножницы.
  • Обычной карандаш либо маркер.
  • Транспортир.
  • Длинноватая линейка.
  • Водянистый клей.
  • Кисточка.

Аннотация

  1. Если у вас есть принтер, то можно распечатать шаблон сходу на листе, но его полностью можно начертить без помощи других. Пятиугольники строятся при помощи транспортира и линейки, угол меж примыкающими линиями должен составлять ровно 108 о, подбирая длину грани можно сделать большой либо небольшой додекаэдр. Развертка представляет собой 2 соединенных «цветка», состоящих из 6 фигур. Непременно оставьте маленькие припуски, они необходимы для склеивания.
  2. Аккуратненько вырежьте заготовку ножницами либо ножиком на особом резиновом коврике, чтоб не разрушить поверхность стола. Дальше прогуляйтесь по местам сгибов острым углом линейки, это приметно облегчит сборку фигуры и сделает грани более осторожными.
  3. При помощи кисточки нанесите на припуски незначительно клея и соберите фигуру подгибая края вовнутрь. Если вы собрались сделать додекаэдр своими руками, а под рукою не оказалось даже скотча, вырежьте припуски одной половины шаблона в виде удлиненных треугольников, а на сгибах 2-ой части сделайте маленькие разрезы. Потом просто воткните краи в пазы, и конструкция будет достаточно крепко держаться.

Готовую фигуру можно разрисовать либо украсить наклейками. Модель огромного размера можно перевоплотить в уникальный календарь, ведь количество сторон соответствует количеству месяцев в году. Если вы увлекаетесь японским прикладным искусством, можно сделать додекаэдр своими руками в технике модульного оригами.

  1. Подготовьте 30 листов обыкновенной офисной бумаги. Отлично если они будут цветными и обоесторонними, можно избрать несколько цветов.
  2. Изготовка модулей. На уровне мыслей расчертите лист на четыре однообразные полосы и сложите гармошкой. Загните углы в на одну сторону в обратных направлениях, получившаяся фигура должна припоминать параллелограмм. Осталось перегнуть заготовку по недлинной диагонали. Сделайте 30 модулей и приступайте к сборке.
  3. Додекаэдр имеет 10 узлов, каждый собирается из 3-х частей. Подготовьте все части и вложите их друг в друга. Чтоб модули не разъезжались, фиксируйте соединения скрепками, когда вы вполне соберете фигуру, их можно будет убрать.

Когда только вы освоите понравившуюся вам технику, можно обучить собирать додекаэдр своими руками вашего малыша либо товарища. Ведь изготовка больших фигур не только лишь отлично развивает моторику пальцев, да и сформировывает пространственное воображение.

Додекаэдром называется правильный многогранник, составленный из двенадцати правильных пятиугольников. Эта эффектная объемная фигура обладает центром симметрии, называемым центром додекаэдра. Кроме того, в ней присутствуют пятнадцать плоскостей симметрии (в каждой грани любая из них проходит через середину противоположного ребра и вершину) и пятнадцать осей симметрии (пересекающих середины параллельных противолежащих ребер). Каждая из вершин додекаэдра является вершиной трех пятиугольников правильной формы.

Свое название конструкция получила по количеству входящих в нее граней (традиционно древние греки давали многогранникам имена, отображающие число граней, составляющих структуру фигуры). Таким образом, понятие «додекаэдр» образовано из значений двух слов: «додека» (двенадцать) и «хедра» (грань). Фигура относится к одному из пяти Платоновых тел (наряду с тетраэдром, октаэдром, гексаэдром (кубом) и ). Интересно, что согласно многочисленным историческим документам, все они активно использовались жителями Древней Греции в виде настольных игральных костей и изготавливались из самого различного материала.

Правильные многогранники всегда привлекали людей своей красотой, органичностью и необыкновенным совершенством форм, но додекаэдр имеет особую историю, которая из года в год обрастает все новыми, иногда совершенно мистическими, фактами. Представители многих цивилизаций усматривали в нем сверхъестественную и таинственную сущность, утверждая, что: «Из числа двенадцать произрастает многое». На территориях древних разрушенных государств до сих пор находят маленькие фигурки в виде додекаэдров, выполненные из бронзы, камня или кости. Кроме того, при раскопках на землях современной Англии, Франции, Германии, Венгрии, Италии археологи обнаружили несколько сотен так называемых «римских додекаэдров», датирующихся II-III-м веками нашей эры. Основные размеры фигурок составляют от четырех до одиннадцати сантиметров, причем отличаются они самыми невероятными узорами, текстурами и техникой исполнения. Выдвинутая еще во времена Платона версия о том, что Вселенная представляет собой огромного размера додекаэдр, нашла подтверждение уже в начале XXI -го века. После тщательного анализа данных, полученных при помощи WMAP(многофункционального космического аппарата NASA), ученые согласились с предположением древнегреческих астрономов, математиков и физиков, в свое время занимавшихся вопросами изучения небесной сферы и ее строением. Более того, современные исследователи считают, что наша Вселенная представляет собой бесконечно повторяющийся набор додекаэдров.

Как сделать правильный додекаэдр своими руками

Сегодня конструкция данной фигуры нашла свое отображение во многих вариантах художественного творчества, архитектуре и строительстве. Народные умельцы изготавливают из цветной или белой бумаги необыкновенные по красоте оригами в виде ажурных додекаэдров, а из картона делают оригинальные и прочее). В продаже можно приобрести уже готовые наборы, содержащие все необходимое для изготовления сувениров, но наиболее интересно произвести весь процесс работы своими руками, начиная от построения отдельных деталей и заканчивая сборкой готовой конструкции.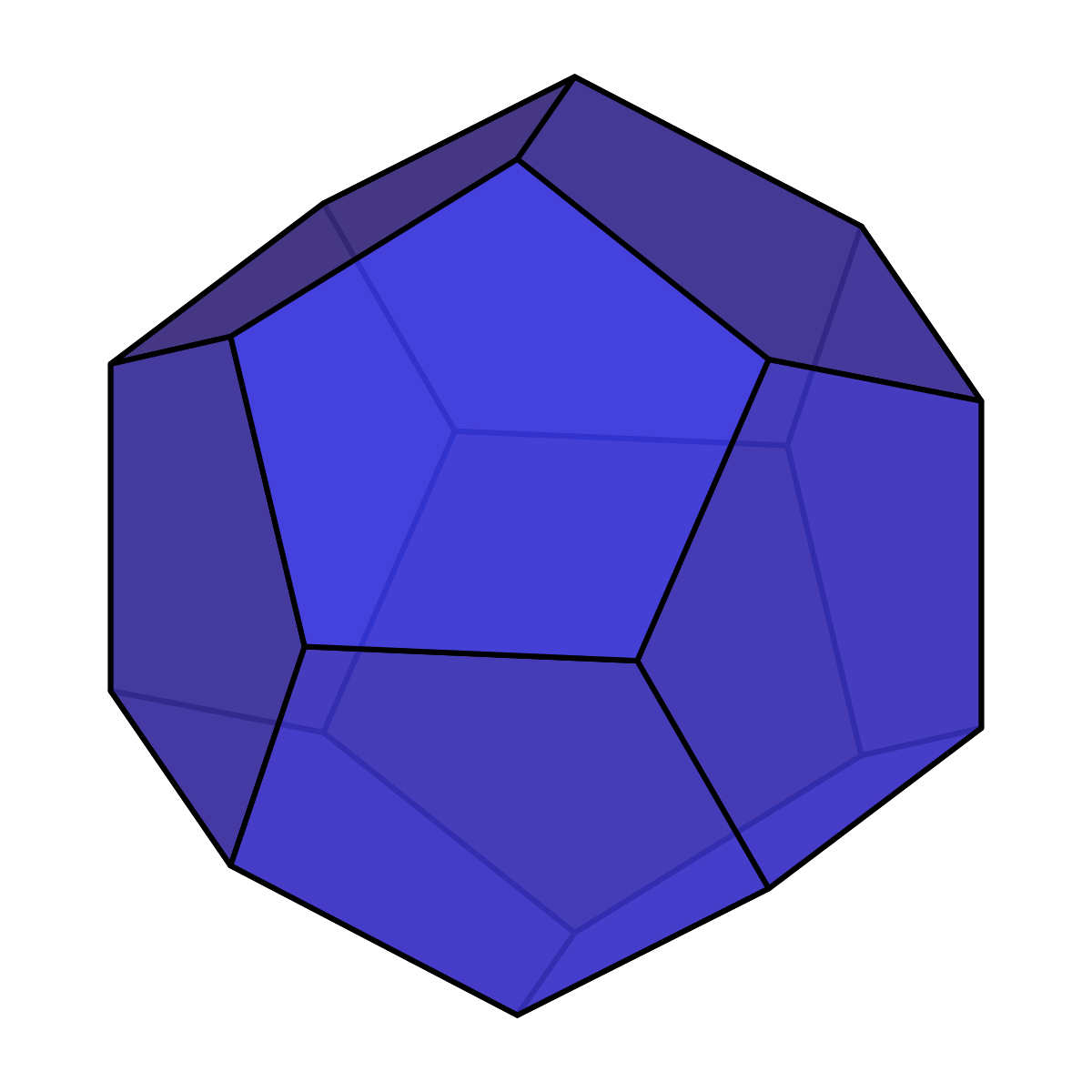

Материалы:

Для того, чтобы сделать правильный додекаэдр из картона, необходим собственно сам материал и подручные средства:

  • ножницы,
  • карандаш,
  • ластик,
  • линейка,
  • клей.

Хорошо иметь тупой нож или какое-либо приспособление для загибания припусков, но если их нет, то вполне подойдет металлическая линейка или те же ножницы.

Как сделать звездчатый додекаэдр

Звездчатые додекаэдры имеют более сложную конструкцию по сравнению с обычными. Эти многогранники подразделяются на малый (первого продолжения), средний (второго продолжения) и большой (последняя звездчатая форма правильного додекаэдра). Каждый из них отличается своими особенностями построения и сборкой. Для работы Вам потребуются те же материалы и инструменты, что и для изготовления стандартного додекаэдра. Если Вы решили сделать первый вариант (малый додекаэдр), то необходимо построить чертеж первого элемента, который станет основой для всей конструкции (в дальнейшем производится ее склеивание или сборка деталей при помощи скрепок).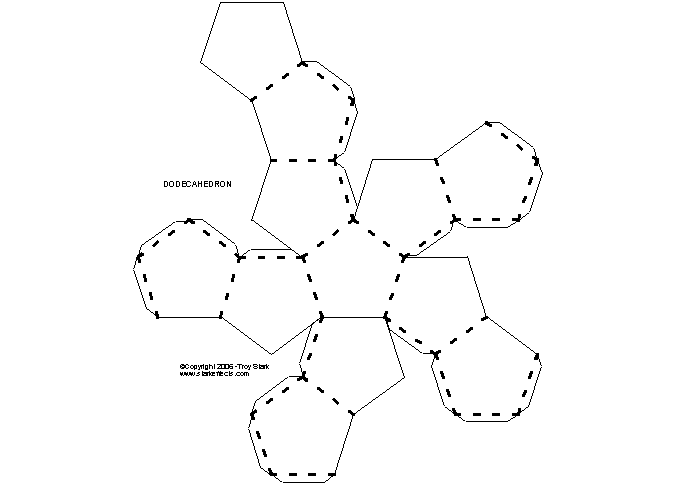

Додекаэдр — это многогранник, состоящий из 12 одинаковых пятиугольников. Это базовая фигура для множества поделок: от настольных календарей до ажурных подвесных фонариков.

Есть и другие методы. Например, пятиугольник можно построить с помощью транспортира, но точности он не гарантирует. Наиболее легий способ — взять готовую схему, распечатать ее и по этой «выкройке» уже мастерить из подходящей бумаги поделку. Но этот способ, несмотря на простоту, подходит не всегда — ведь иногда нужно сделать додекаэдр какого-то конкретного размера. Можно увеличить один пятиугольник до нужного масштаба и распечатать только его, затем построить фигуру по схеме ниже.

Но «выкройка» — это еще не готовая поделка. Как сделать додекаэдр из бумаги? Для этого понадобятся:

1. Бумага, подходящая по плотности. Она не должна быть слишком тонкой или же слишком толстой — желательно 220 г/м², именно такой плотностью обладает картон, который продают в детских наборах. Хотя из толстого картона вполне можно создавать объемные фигуры, нужно только предварительно обработать все сгибы — слегка надрезать или хорошо продавить, чтобы они хорошо и ровно сгибались.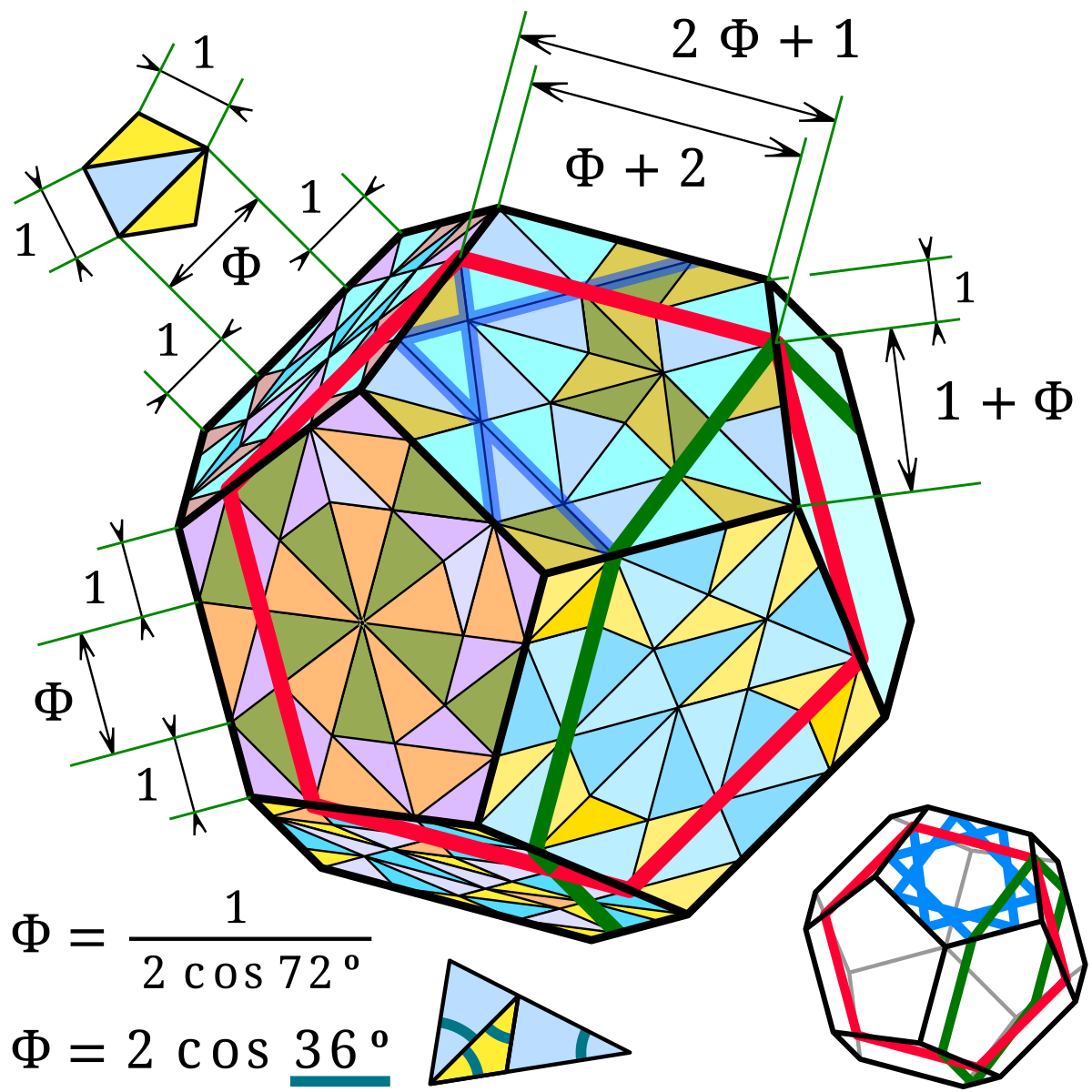

2. Ножницы, вязальная спица или канцелярский нож

Советы по изготовлению додекаэдра

Бумагу в местах сгибов желательно слегка продавить спицей, тупой стороной или чем-то острым, но не режущим. Аккуратные ровные сгибы — половина успеха.

Если клея под рукой нет, додекаэдр можно собрать, как конструктор, сделав надрезы по сгибам, а затем просто вставив стороны одна в другую.

Если вы собираете додекаэдр в модульной технике (инструкция ниже), то места соединений желательно проклеивать или закреплять скрепками, поскольку конструкция станет устойчивой только после закрепления последнего модуля.

Додекаэдр в технике оригами

Модуль оригами — отличная основа для додекаэдра. Как сделать додекаэдр из бумаги в модульной технике? Понадобится 30 прямоугольных или квадратных листов бумаги. Каждый из листочков складывается пополам, затем каждую половинку нужно отогнуть в противоположную сторону — получится «гармошка» в четыре сложения. Иногда, если лист не квадратный, делают «гармошку» в три сложения. В итоге у вас в руках узкая промоугольная полоска. Затем с каждой стороны прямоугольника по узкой стороне нужно отогнуть уголок. Уголки складываются в одну сторону — это будущие крепления, которые будут заправляться в «гармошку». Затем согните модуль вовнутрь наискосок по диагонали от маленьких боковых уголков. Таким образом, один модуль для оригами додекаэдра — трехмерный, он включает два ребра будущей фигуры и уголки. Когда все модули готовы, можно начинать сборку.

Сборка начинается с одного узла, для которого необходимо взять три модуля. На рисунке ниже это голубой, розовый и желтый модули оригами. Схемы сборки достаточно просты, и с такими фигурами легко справляются даже начинающие.

Какие поделки можно сделать на основе додекаэдра?

Каждая сторона додекаэдра из бумаги — это плоский пятиугольник, который сам по себе может являться основой для самых разных и причудливых форм. Например, на фото ниже пятиугольник заменен пятиконечнй звездой. Ребра в такой фигуре отсутствуют, хотя предполагаются. Как сделать додекаэдр из бумаги в виде звезды? Замените в развертке, представленной выше, каждый пятиугольник необходимой пятиконечной фигурой и соедините их не по ребрам, а по вершинам.

На этом фото представлен звездчатый додекаэдр. В основе каждого «луча» лежит все тот же пятиугольник.

Вместо пятиугольных пирамид может быть выполнена любая объемная фигура.

На фото ниже в качестве пятиугольников выступают более сложные модули оригами, схемы которых заинтересовавшиеся этой техникой смогут найти в специальной литературе.

В любом случае освоение даже простейшей схемы сборки додекаэдра уже даст огромные возможности для творчества и поиска своих собственных вариантов.

Додекаэдр: 12-гранная форма с 12-буквенным именем

Учить новое слово каждый день — довольно хорошая привычка. (Владелец Гарфилда так считает). И в этом духе вот забавный математический термин, о котором вы, возможно, не знали: «Додекаэдр». Что это значит? Мы рады, что вы спросили. Вот 12 вещей, которые нужно знать об этом.

1. Додекаэдры — разновидность многогранников

Треугольники и квадраты — это многоугольники, двумерные формы, образованные прямыми линиями. А теперь просто ради удовольствия, давайте продолжим и добавим третье измерение.Многогранник — это трехмерный объект, состоящий из многоугольных граней. Итак, в то время как квадрат — это многоугольник, куб — это многогранник. Помните это для вашей следующей вечеринки с вином и сыром (« Эй, можно мне еще этих многогранников чеддера? »).

2. Додекаэдры имеют 12 пятиугольных граней

Как вы знаете, если вы когда-нибудь были в Вашингтоне, округ Колумбия, пятиугольники — это двумерные формы с пятью прямыми краями, которые образуют пять углов на углах. Додекаэдры (произносится как dow · deh · kuh · hee · druhns) — это трехмерные тела, содержащие дюжину плоских граней — все они имеют форму пятиугольника.

3. Имя «Додекаэдр» имеет греческие корни.

Пора заставить улыбнуться папа из «Моя большая греческая свадьба».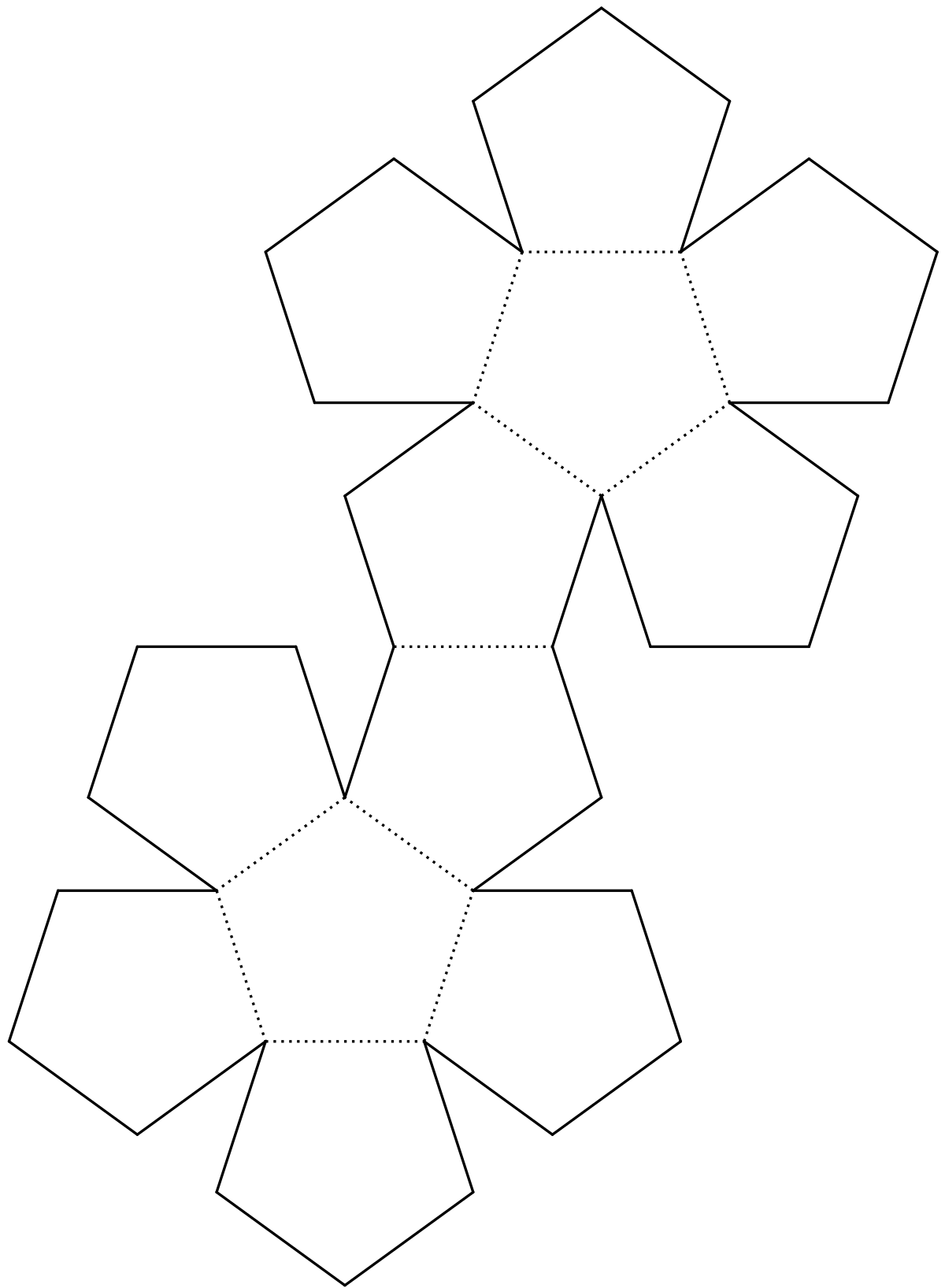 «Додекаэдр» происходит от греческих слов «додека» и «хедра», что означает «12» и «место или основание» соответственно.

4. Каждый из них содержит «ребра» и «вершины»

«Ребра» — это просто; это линии, на которых встречаются два многоугольника (квадраты, треугольники и т. д.) на многограннике. Вершины — или «вершины» — это заостренные биты, в которых сходятся три или более граней.Каждый додекаэдр с одинаковыми гранями будет иметь 30 ребер и 20 вершин.

5. Так называемый «обычный» додекаэдр — часть элитной группы …

Проверяйте свои копрологические шутки у двери. Многогранник считается «правильным», если (а) все его грани — одинаковые многоугольники; (б) все углы выглядят одинаково; и (c) края равны по длине. Математики доказали, что существует всего пять видов правильных многогранников. Вместе они известны как пять Платоновых тел.«И правильный додекаэдр оказывается одним из них.

6. … Но это не обязательно самый эффектный элемент

Кубы (также известные как« правильные шестигранники ») — самые известные Платоновы тела, без всякого сомнения. также узнайте тетраэдр, пирамиду с треугольным основанием. Далее идет октаэдр, восьмиугольная красота, похожая на алмаз. Наконец, есть икосаэдр с его 20 — сосчитайте их, 20 — треугольными гранями.

7. Можно заполнить одно другими платоновыми телами

Вот крутой трюк: если объединить пять тетраэдров вместе и использовать расположение их вершин для создания новых многоугольных граней, вы можете получить идеальный додекаэдр.Точно так же существует несколько различных способов использовать соединения кубов в качестве основы для додекаэдров. Пространственные махинации — это очень весело.

8. Додекаэдры могут делать то, что не могут сделать другие формы

Если бы вы жили на гигантском додекаэдре, как бы вы переместились из точки A в точку B? Установить курс может быть проще, чем вы думаете. В 2018 году математики Джаядев Артреа, Дэвид Авликино и Пэт Хупер показали, что можно провести прямой путь на додекаэдре, который начинается в одной вершине и возвращается в ту же точку, не поворачиваясь и не проходя через другие углы. Однако на кубе, тетраэдре, октаэдре или икосаэдре не было бы возможности совершить этот подвиг.

9. Древние римляне делали бронзовые додекаэдры

С 1739 года археологи обнаружили десятки небольших искусственных додекаэдров в местах, когда-то оккупированных Римской империей. Обычно сделанные из бронзы, эти объекты полые, у них есть выступы на вершинах, а каждая грань имеет круглое отверстие в центре. Извлеченные к настоящему времени образцы были построены между 1 и 500 годами C.E. Мнения об их функции расходятся; насколько нам известно, маленькие странности могли быть оружием, игральными костями, подсвечниками или чем-то еще.

10. Форма жизни в форме додекаэдра существовала 100 миллионов лет назад

Braarudosphaera bigelowii была разновидностью водорослей, обитавших в эпоху динозавров. Обнаруженный в геологических местах по всему миру, микроорганизм был покрыт пятиугольной чешуей, расположенной вместе в виде додекаэдра. Жаль, что мы никогда не встречали динозавров с таким диким строением тела.

11. «Подземелья и драконы». Игроки используют кости додекаэдра

В этой ролевой игре в жанре фэнтези участники бросают кости разных форм и размеров. Игральные кости D12, незаменимые во многих ситуациях, связанных с большим оружием, представляют собой мини-додекаэдры.

12. В «Таинстве Тайной вечери» Сальвадора Дали есть додекаэдр на заднем плане

Поскольку у Христа была дюжина учеников, а в году дюжина месяцев, Дали чувствовал, что «12 пятиугольников додекаэдра» будут идеально подходить (тематически) для этой сюрреалистической картины, написанной им в 1955 году.

Додекаэдр — Определение, формулы, свойства, примеры и практические вопросы

Додекаэдр — это трехмерная фигура, имеющая двенадцать граней пятиугольной формы. Все грани имеют плоскую двумерную форму. Платоновых тел пять, и додекаэдр — одно из них. Платоновы тела — это выпуклые многогранники, в которых грани составлены из конгруэнтных правильных многоугольников с одинаковым количеством граней, пересекающихся в каждой из вершин. Додекаэдр состоит из 12 совпадающих пятиугольников с тремя пятиугольными гранями, пересекающимися в каждой из 20 вершин.Есть два типа додекаэдра — правильный и неправильный додекаэдр.

Что такое додекаэдр?

Додекаэдр происходит от греческого слова «dōdeka» означает «12», а «hédra» означает «грань или сиденье», что указывает на то, что это многогранник с 12 сторонами или 12 гранями. Следовательно, любой многогранник с 12 сторонами можно назвать додекаэдром. Он состоит из 12 пятиугольных граней. Определение додекаэдра можно лучше понять с помощью этой иллюстрации.

Предположим, что вы живете в одном из платоновых тел, и у вас есть дом в одной из вершин. Ваши соседи живут в других вершинах. Каждое утро вы бежите трусцой, вы бежите по прямой, никогда не поворачиваете и не меняете свой путь. Можно ли пойти по прямой и вернуться в свой дом, не проходя через дома соседей? Скорее всего, вы подумаете, что ответ — нет!

Более 2000 лет математики знали о платоновых телах, но недавно группа из трех математиков — Джаядев Атрейя, Дэвид Авликино и Патрик Хупер нашла решение этой проблемы в виде додекаэдра. У додекаэдра 31 такой путь.

Сетка из додекаэдра

Сеть додекаэдра помогает нам идентифицировать грани, ребра и вершины. Вы можете создать свой собственный додекаэдр или форму додекаэдра из сети додекаэдров, показанной ниже.

Шаги для создания формы додекаэдра:

  • Возьмите распечатку сетки додекаэдра.
  • Сложите по внутренним линиям.
  • Склейте линии того же цвета, чтобы сформировать выпуклый додекаэдр.

Правильный додекаэдр

У правильного додекаэдра 12 правильных пятиугольных сторон. Вы можете видеть на изображении сети додекаэдра, показанном выше, что у додекаэдра есть 12 пятиугольных сторон.

Площадь поверхности додекаэдра ≈ 20,64 × a 2 квадратных единиц (где a — длина одной стороны)

Объем додекаэдра ≈ 7,66 × a 3 кубических единиц (где a — длина одной стороны)

Свойства додекаэдров

Давайте узнаем некоторые важные свойства (стороны, ребра, формы, вершины, углы), связанные с додекаэдром .

  • Стороны — Додекаэдр имеет 12 пятиугольных сторон.
  • Ребра — Додекаэдр имеет 30 ребер.
  • Vertices — он имеет 20 вершин (угловых точек), и в каждой вершине пересекаются 3 ребра.
  • Имеет 160 диагоналей.
  • Сумма углов в каждой вершине составляет 3 x 108 ° = 324 °.
  • Углы — угол между сторонами пятиугольника: 108 ° и угол пересечения двух смежных граней (двугранный угол) : 116.56505 °
  • Формы — Формы додекаэдра можно увидеть во многих реальных ситуациях, таких как римский додекаэдр, игральные кости додекаэдра и т. Д.

Важные примечания

  • Тетраэдр, куб, октаэдр, икосаэдр и додекаэдр — единственные 5 платоновых тел.
  • Икосаэдр имеет максимальное количество граней (т.е. 20).
  • Додекаэдр и икосаэдр имеют одинаковое количество ребер, т.е. 30.
  • Икосаэдр называется двойственным к дедекаэдру, так как оба они имеют одинаковое количество ребер.Икосаэдр — это платоновая форма с наибольшим количеством граней и наибольшим объемом среди всех платоновых тел.

Аналитический центр

  • Согласно греческому философу Платону, тетраэдр символизирует огонь; куб символизирует землю; Точно так же все платоновы тела что-то символизируют. Вы знаете, что символизирует додекаэдр?

Статьи, связанные с додекаэдром

Ознакомьтесь с этими интересными статьями о додекаэдре.Нажмите, чтобы узнать больше!

Часто задаваемые вопросы о додекаэдре

Что такое правильный додекаэдр?

Правильный додекаэдр — это додекаэдр с 12 пятиугольными гранями одинаковой длины. Это одно из пяти платоновых тел. Он имеет в общей сложности 20 вершин, 30 ребер и 160 диагоналей, включая 60 диагоналей граней и 100 диагоналей пространства.

Что означает икосаэдр?

Икосаэдр — это многогранник с 20 гранями. Это платоновое тело с 5 равносторонними треугольниками, расположенными в каждой из 12 вершин.

Является ли додекаэдр двумерной формой?

Нет, додекаэдр — это не двумерная форма. Додекаэдр — это трехмерная форма, также известная как платоновое твердое тело с двенадцатью гранями. Каждая из этих граней представляет собой правильный пятиугольник.

Как называется 3D Пентагон?

Трехмерная форма, состоящая из пятиугольников, представляет собой правильный додекаэдр. Все грани правильного додекаэдра имеют форму пятиугольника.

Кто изобрел додекаэдр?

Додекаэдр был изобретен пифагорейцами.

Сколько градусов у додекаэдра?

Размер двугранного угла додекаэдра составляет 116,565 °.

Является ли додекаэдр многогранником?

Да, додекаэдр — это многогранник, потому что многогранник — это твердое тело, все грани которого являются многоугольниками. Все грани додекаэдра — пятиугольники, которые представляют собой правильный пятиугольник.

математиков сообщают о новом открытии о додекаэдре

Математики потратили более 2000 лет на анализ структуры пяти Платоновых тел — тетраэдра, куба, октаэдра, икосаэдра и додекаэдра — но мы еще многого о них не знаем. .

Теперь трио математиков решили один из самых основных вопросов о додекаэдре.

Предположим, вы стоите в одном из углов платонового тела. Есть ли какой-нибудь прямой путь, который в конечном итоге вернет вас к исходной точке, не проходя через какие-либо другие углы? Для четырех Платоновых тел, построенных из квадратов или равносторонних треугольников — куба, тетраэдра, октаэдра и икосаэдра — математики недавно пришли к выводу, что ответ отрицательный.Любой прямой путь, начинающийся из угла, либо попадет в другой угол, либо будет извиваться вечно, не возвращаясь домой. Но с додекаэдром, состоящим из 12 пятиугольников, математики не знали, чего ожидать.

Джаядев Атрейя, Дэвид Авликино и Патрик Хупер показали, что на додекаэдре действительно существует бесконечное количество таких путей. Их статья, опубликованная в мае в Experimental Mathematics , показывает, что эти пути можно разделить на 31 естественное семейство.

Решение потребовало современных методов и компьютерных алгоритмов. «Двадцать лет назад [этот вопрос] был абсолютно недоступен; 10 лет назад для написания всего необходимого программного обеспечения потребовались бы огромные усилия, поэтому только сейчас все факторы сошлись воедино », — написал Антон Зорич из Института математики Жюссье в Париже в электронном письме.

Проект начался в 2016 году, когда Атрейя из Вашингтонского университета и Ауликино из Бруклинского колледжа начали играть с коллекцией вырезок из картона, которые складываются в платоновые твердые тела.Когда они строили различные твердые тела, Авликино пришло в голову, что недавние исследования плоской геометрии могут оказаться именно тем, что им нужно, чтобы понять прямые пути на додекаэдре. «Мы буквально собирали эти вещи воедино», — сказал Атрейя. «Так что это было своего рода праздное исследование и возможность».

Вместе с Хупером из Городского колледжа Нью-Йорка исследователи выяснили, как классифицировать все прямые пути от одного угла до самого себя, избегая других углов.

Их анализ — «элегантное решение», — сказал Говард Мазур из Чикагского университета. «Это одна из тех вещей, где я могу без колебаний сказать:« Боже мой, если бы я сделал это! »»

Скрытые симметрии

Хотя математики размышляли о прямых путях на додекаэдре более века , в последние годы наблюдается возрождение интереса к этой теме после улучшения понимания «поверхностей перевода». Это поверхности, образованные путем склеивания параллельных сторон многоугольника, и они оказались полезными для изучения широкого круга тем, связанных с прямыми путями на фигурах с углами, от траекторий бильярдного стола до вопроса о том, когда один источник света может осветить весь зеркальная комната.

Во всех этих задачах основная идея состоит в том, чтобы развернуть вашу фигуру таким образом, чтобы упростить изучаемые пути. Итак, чтобы понять прямые пути на платоновом твердом теле, вы можете начать с разрезания достаточного количества краев, чтобы твердое тело лежало плоско, образуя то, что математики называют сетью. Одна сетка для куба, например, представляет собой Т-образную форму, состоящую из шести квадратов.

Бумажный додекаэдр, построенный в 2018 году Дэвидом Авликино и Джаядевым Атрейей, чтобы показать, что прямые пути от вершины к самой себе, избегая других вершин, на самом деле возможны.Фотография: Патрик Хупер

Представьте, что мы выровняли додекаэдр и теперь идем по этой плоской форме в каком-то выбранном направлении. В конце концов, мы наткнемся на край сети, и в этот момент наш путь перейдет к другому пятиугольнику (тот, который был приклеен к нашему текущему пятиугольнику, прежде чем мы разрежем додекаэдр). Каждый раз, когда путь прыгает, он также поворачивается на 36 градусов.

Чтобы избежать всех этих скачков и поворотов, когда мы ударяемся о край сети, мы могли бы вместо этого приклеить новую повернутую копию сети и продолжить движение прямо в нее.Мы добавили немного избыточности: теперь у нас есть два разных пятиугольника, представляющие каждый пятиугольник на исходном додекаэдре. Итак, мы усложнили наш мир, но наш путь стал проще. Мы можем добавлять новую сеть каждый раз, когда нам нужно выйти за пределы нашего мира.

Додекаэдр — обзор

8.1 Додекаэдр

Есть много соединений лантаноидов, имеющих координационные полиэдры, близкие к додекаэдру с треугольными гранями. Остается большой интерес к различным окружениям и комбинациям лигандов, для которых додекаэдрическое расположение является благоприятным.

Структура Dy (NTA) (H 2 O) 2 состоит из атомов диспрозия с пятью ацетатными атомами кислорода, двумя молекулами воды и одним атомом азота, расположенными по углам искаженного додекаэдра. Каждый нитрилотриацетатный лиганд представляет собой гексадентат с одним ацетатным атомом кислорода, некоординированным с любым атомом металла, и двумя карбоксилатными атомами кислорода, координированными с атомами металла в соседних молекулах. Таким образом, структура является полимерной [84].

Полимерные структуры, содержащие додекаэдрически координированные атомы металлов, встречаются среди карбоксилатов более тяжелых лантаноидов.Эрбий в [Er (HOCH 2 COO) — (OCH 2 COO) (H 2 O)] H 2 O координирован с восемью атомами кислорода, представленными гидроксиацетатом, оксиацетатом и молекулой воды [89 ]. Ацетатные группы действуют как мостиковые лиганды, и результирующая структура показана на рис. 5.16.

Рис. 5.16. Проекция структуры Er (HOCH 2 COO) (OCH 2 COO) (H 2 O) · H 2 O.

(из Grenthe [89])

Додекаэдры встречаются попарно, разделяя пара атомов кислорода у общего края, и их форма искажена от идеальной.Таким образом, есть две пересекающиеся трапеции с углами θ A = 34,5 ° и 37,4 °; θ B = 73,2 ° и 69,5 °. Есть два типа атомов металлов в кристаллической структуре [88] Er (HOCH 2 COO) 3 · 2H 2 O. Каждый металл связан с восемью атомами кислорода, образуя искаженный додекаэдр. Один Er находится в форме комплексного аниона [Er (HOCH 2 COO) 4 ] — , а другой Er находится в форме комплексного катиона, [Er (HOCH 2 COO) 2 (H 2 O) 4 ] + .И комплексный катион, и анион связаны друг с другом в двух измерениях водородными связями, образующими слои с плоскостью « ab ». Гликолятные лиганды образуют хелаты по m краям обоих додекаэдров.

Комплекс (NH 4 ) 3 CeF 7 · H 2 O существует в виде димера, в котором додекаэдры имеют общее ребро [82]. Каждый атом церия окружен восемью атомами фтора, образуя искаженный додекаэдр. Два додекаэдра соединены вдоль ребра, образуя центросимметричный ион [Ce 2 F 14 ] 6-, как показано на рис.5.17.

Рис. 5.17. Структура димерного аниона в (NH 4 ) 3 CeF 7 · H 2 O (из Райана и Пеннемапа [82]).

(от Ryan and Pennemap [82])

Тетракишексафторацетилацетонаты Eu и Y изоморфны и имеют додекаэдрическое расположение D 2 с хелатными кольцами, охватывающими g-края многогранника. В этой структуре, как и в случае NH 4 [Pr (TTA) 4 ] · H 2 O, кольца соединяют между собой трапеции додекаэдра.Структура иттриевого комплекса соответствует сильной ионной паре с ионом цезия, окруженным восемью атомами фтора из двух соседних фрагментов Y (HFA) 4–. Координационный додекаэдр в комплексе [Y (HFAcAc) 4 ] — , если смотреть вниз по двойной оси через ион иттрия, показан на рис. 5.18.

Рис. 5.18. Координационный додекаэдр в ионе тетракис (гексафторацетилацетонато) иттрата (III), если смотреть вниз по двойной оси через ион иттрия.

(перепечатано с разрешения Bennett, M.J., F.A. Cotton, P. Legzdins, S.J. Липпард, 1968, Неорг. Chem. 7, 1770–1776) Copyright © 1968

В комплексе NH 4 [Ho (tropolanto) 4 ] м пересечены края, так как комплекс имеет небольшой прикус [125]. Аналогичная ситуация с разделением m ребер встречается в тетракис [4,4,4-трифтор-1- (2-тиенил) -1,3-бутандион] церия (III) изохинолиния, и додекаэдр искажается образованием водорода связь иона изохинолиния с одним из хелатных атомов кислорода [126].

В целом, большинство комплексов типа [M (бидентатный) 3 (единичный) 2 ] n + имеют квадратную антипризматическую стереохимию. Из этого обобщения есть некоторые исключения. Комплекс Nd (TTA) 3 (opph 3 ) 2 имеет додекаэдрическую конфигурацию [127] с двумя хелатными кольцами, охватывающими 9 ребер, и третьим, охватывающим ребро m, как показано на рис. 5.19.

Рис. 5.19. Координационный многогранник в Nd (TTA) 3 (Opph 3 ) 2 .

(перепечатано с разрешения Leipoldt, JG, LDC Bok, AE Laubscher и SS Bosson, 1975, J. Inorg. Nucl. Chem. 37, 2477–2480) Copyright © 1975

Состав Pr 2 (fod) 6 · 2H 2 O — интересное соединение, содержащее восемь димерных координационных групп [83]. Комплекс имеет один атом празеодима додекаэдрической конфигурации, а второй атом металла имеет двояковую тригонально-призматическую структуру. Хелатные кольца очень похожи на таковые в семикоординатном комплексе Pr 2 ( DPM ) 6 ​​.

Открытие додекаэдра встряхивает каркас пяти платоновых тел — сейчас. Powered by Northrop Grumman

Есть пять Платоновых тел: тетраэдр, шестигранник (куб), октаэдр, додекаэдр и икосаэдр. Это уникальная группа трехмерных фигур с одинаковыми многоугольниками на каждой грани и одинаковым количеством многоугольников, пересекающихся в каждом углу. Эти твердые тела с одной и той же поверхностью не новы для математиков — их называют «платоническими», потому что афинский философ Платон, как известно, связал их с элементами природы, — но они по-прежнему остаются источником математической загадки.Теперь новое открытие додекаэдра встряхивает структуру пяти твердых тел с перестановкой путей.

Цельное золото

Итак, что отличает Платоново твердое тело от других форм? Все дело в повторении. Каждое Платоново тело имеет один и тот же многоугольник на каждой грани и одинаковое количество многоугольников, соприкасающихся с каждым углом (который называется вершиной), а внутренние углы этих точек встречи составляют в сумме менее 360 градусов.

В качестве простого примера рассмотрим куб.У него шесть сторон, каждая из которых представляет собой квадрат, с тремя квадратами, сходящимися в каждом углу. Каждый внутренний угол равен 90 градусам, что означает, что сумма в каждой вершине равна 270 градусам. Три из пяти других Платоновых тел — тетраэдр, октаэдр и икосаэдр — имеют треугольники на каждой грани, а додекаэдр — пятиугольники.

Вот краткая разбивка:

  • Тетраэдр — четыре грани треугольника, три треугольника пересекаются в каждом углу с комбинированными углами 180 градусов
  • Шестигранник (куб) — шесть квадратных граней, три квадрата пересекаются в каждом углу с комбинированными углами 270 градусов
  • Октаэдр — восемь граней треугольника, четыре треугольника пересекаются в каждом углу с комбинированными углами 240 градусов
  • Додекаэдр — 12 граней пятиугольника, три пятиугольника встречаются в каждом углу с комбинированными углами 324 градуса
  • Икосаэдр — 20 треугольных граней, пять треугольников пересекаются в каждом углу с комбинированными углами 300 градусов

Пятерка для драки

Почему пять? Почему не десять, двадцать или тысяча Платоновых тел?

Ответ прост, если не сразу очевиден: внутренние углы.Рассмотрим шестиугольник с внутренними углами 120 градусов на каждом углу. Чтобы создать трехмерный многоугольник, по крайней мере три грани должны соприкоснуться, то есть внутренний угол одинаковых вершин шестиугольника составляет 360 градусов (3 × 120), и форма становится плоской. Та же проблема возникает, если мы добавляем больше углов к существующей линии Платоновых тел — в то время как три встречающихся пятиугольника дают общий угол 324 градуса по 108 градусов каждый, добавление еще одного угла увеличивает его до 432 градусов и делает невозможным создание связного многоугольника. .

Хотя эту угловую проблему можно решить, изменив форму некоторых сторон, чтобы внутренняя сумма была меньше 360 градусов, твердое тело больше не является однородным. Несмотря на математические попытки доказать обратное на протяжении двух тысячелетий, существует только пять форм, которые удовлетворяют всем трем условиям: идентичные грани, равномерные угловые соединения и объединенные углы вершин менее 360 градусов.

Найдено в переводе

Несмотря на то, что времени для изучения пяти Платоновых тел достаточно, вопросы все еще остаются.Один из самых популярных центров по углам и тропам: можно ли стоять в углу любого Платонического тела, идти по прямой и вернуться в исходную точку, не проходя по пути через какие-либо другие углы? Недавние исследования показали, что не существует таких угловых или «геодезических» путей через тетраэдры, октаэдры, икосаэдры или кубы. Но как насчет додекаэдров в виде пятиугольника?

Как оказалось, существует бесконечное количество способов начать с угла, пройти через додекаэдр и вернуться туда, где вы начали, и все это, не пересекая свой собственный путь.Исследование, опубликованное в журнале Experimental Mathematics, три математика — Джаядев Атрейя, Дэвид Авликино и Патрик Хупер — обнаружили «ровно 31 класс эквивалентности замкнутых седловых соединений», которые можно использовать в качестве основы для неперекрывающихся маршрутов. Они полагались на использование компьютерных алгоритмов для создания так называемых «поверхностей перевода».

Эти поверхности начинаются с Платоновых тел, которые были разорваны по углам и стали плоскими. Каждая итерация этой плоской поверхности называется «сетью» и предлагает исходную точку для нашего потенциального Платонического пути.Когда этот путь достигает края сети, добавляется еще одна цепь, повернутая на несколько крат 36 градусов, чтобы представить следующую цепь вокруг додекаэдра. Разложите 10 цепей, и вы охватите все 360 градусов, это означает, что 11-я сеть фактически такая же, как первая, и может быть соединена с соответствующим аналогом на первой цепочке для создания полной поверхности перемещения.

Используя передовое компьютерное моделирование, команда смогла вычислить все возможные пути из всех возможных углов и продемонстрировать, что на самом деле существует множество непересекающихся проверенных додекаэдрических маршрутов, которые ведут от одной и той же вершины и обратно.

Формируя будущее

Хотя математическое и статистическое моделирование, лежащее в основе исследования пяти платоновских форм, может не привлекать общественный интерес, как продолжающаяся эволюция более известных теорий квантовой механики и относительности, исследования показывают, что даже хорошо известные и, казалось бы, хорошо изученные фреймворки по-прежнему содержат секреты, которые могут помочь сформировать наше понимание физического мира.

Ознакомьтесь с возможностями карьерного роста в Northrop Grumman, чтобы узнать, как вы можете принять участие в этом увлекательном времени открытий в области науки, технологий и инженерии.

Произошла ошибка при настройке пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка вашего браузера для приема файлов cookie

Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:

  • В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
  • Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
  • Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
  • Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
  • Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файле cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.

Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.

Всплывающий додекаэдр, возраст 5+ | BA Playground

Когда мы обводим наш пятиугольник на картоне, обратите внимание на небольшие промежутки между внешними пятиугольниками.

Когда фигуры плотно прилегают друг к другу, без промежутков между ними и могут покрывать весь лист бумаги (независимо от его размера), это называется «мозаикой». («Плоскость» — это математический термин, обозначающий плоскую двухмерную поверхность, например лист бумаги.)

Пусть ваш ребенок попробует обвести свой пятиугольник так, чтобы фигуры были прямо напротив друг друга (без перекрытия) и были между ними нет зазоров.Не заставляйте их слишком долго пытаться, потому что они быстро поймут, что это невозможно.

Итак, какими формами можно выложить плоскость? Вырежьте разные формы, чтобы попробовать. Также см. Нашу игру BA Playground Cookie Cutter для получения дополнительной информации по этой теме.

Трехмерная форма, такая как ваш всплывающий додекаэдр, называется многогранником. Леонард Эйлер, считающийся одним из величайших математиков всех времен, открыл простую формулу о многогранниках, которую легко проверить даже юным математикам.

Сколько плоских частей пятиугольника у вашего додекаэдра? (Их двенадцать.) Математический термин для этих плоских частей — «лица». Один из способов подумать о количестве граней — это представить, что ваш додекаэдр был кубиком. Насколько высоко вы сможете его пронумеровать?

Теперь посчитайте количество «вершин» вашего додекаэдра. Это острые углы, которые торчат наружу. Их много, так что может помочь раскрасить их маркером на ходу. Всего 20 вершин.

Наконец, посчитайте, сколько у него «ребер». Это прямые части, где встречаются пятиугольники.Опять же, их довольно много, поэтому следите за ними, отмечая их маркером при подсчете.

Вершины отмечены оранжевым, а края — синим.

У вашего додекаэдра 30 ребер.

Итак, что вы получите, если сложите количество граней и вершин, а затем вычтите количество ребер? Наш расчет: 12 + 20 — 30 = 2.

Чтобы понять, почему это примечательно, найдите другие многогранники для изучения. Вы можете этого не осознавать, но, вероятно, у вас дома есть другие многогранники.Игральная кость — это куб, который представляет собой своего рода многогранник. Подсчитайте количество граней, вершин и ребер. У куба 6 граней, 8 вершин и 12 ребер. Снова сложите количество граней и вершин, затем вычтите количество ребер: 6 + 8 — 12 = 2. Мы снова получили 2?

Вы можете найти больше многогранников. Вот еще пара, которую мы нашли.

Красный блок имеет 5 граней, 6 вершин и 9 ребер. Формула Эйлера дает нам 5 + 6 — 9 = 2. Оранжевый блок имеет 8 граней, 12 вершин и 18 ребер. Формула Эйлера дает нам 8 + 12 — 18 = 2.Вы будете получать 2 раза каждый раз!

Будьте осторожны при поиске многогранников. Формула Эйлера применима только к так называемым «выпуклым» многогранникам, то есть к формам, у которых нет ни одной части, вогнутой внутрь. Любой блок изогнутой формы также не является многогранником.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *